Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 10.Problemas - Ex. 60
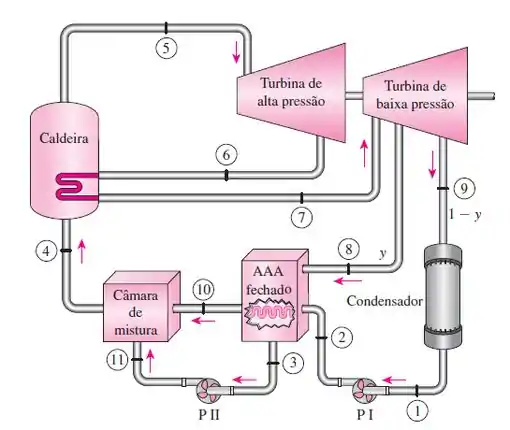
Uma usina de potência a vapor opera no ciclo de Rankine com reaquecimento e regeneração com um aquecedor de água de alimentação fechado. Vapor entra na turbina a 8 MPa e 500 °C com uma vazão de 15 kg/s e é condensado no condensador a uma pressão de 20 kPa. O vapor é reaquecido a 3 MPa até 500 °C. Parte do vapor, extraído da turbina de baixa pressão a 1,0 MPa, é completamente condensado no aquecedor de água de alimentação e bombeado até 8 MPa antes de se misturar à água de alimentação à mesma pressão. Considerando uma eficiência isentrópica de 88% para a turbina e para a bomba, determine (a) a temperatura do vapor na entrada do aquecedor de água de alimentação, (b) o fluxo de massa do vapor extraído da turbina para o aquecedor de água de alimentação, (c) a potência líquida e (d) a eficiência térmica.
Passo 1
Beleza! Então agora o que temos que fazer é pegar o valor das propriedades nos pontos de interesse com o auxílio das tabelas termodinâmicas, então teremos:
Agora, como os líquidos entrando na câmara de mistura possuem a mesma entalpia, então, os pontos 4, 10 e 11 terão a mesma entalpia, dessa forma, temos:
Agora, continuando a análise dos pontos de interesse, temos:
Agora, para encontrar a entalpia real do ponto 6, precisamos primeiro encontrar a entalpia para o caso isentrópico e depois utilizar a relação de eficiência isentrópica para encontrar o valor da entalpia real, dessa forma, assumindo expansão isentrópica para a turbina de alta pressão, temos:
Agora, sabemos que a eficiência isentrópica da turbina de alta pressão será dada por:
Substituindo os valores conhecidos, temos:
Agora, para o ponto 7, temos:
Agora, da mesma forma, vamos repetir a análise isentrópica para a turbina de baixa pressão, então, considerando a expansão 7-8 como isentrópica, temos:
Agora, utilizando a equação de eficiência isentrópica da turbina de baixa pressão, temos:
Substituindo os valores conhecidos, temos:
Agora, com isso, podemos encontrar a temperatura do vapor na entrada do aquecedor de água de alimentação interpolando na tabela do apêndice A:
Passo 2
Vamos continuar nossa análise dos pontos de interesse, agora, ainda para a turbina de baixa pressão, considerando a expansão 7-9 como isentrópica, temos:
E, novamente, utilizando a equação da eficiência isentrópica, temos:
Substituindo os valores conhecidos, temos:
Agora nós vamos calcular o valor dos trabalhos específicos demandados pela turbina para depois encontrar as entalpias na saída de cada uma delas, então, começando pelo trabalho da bomba 1, temos:
Com isso, podemos descobrir o valor da entalpia no ponto 2 aplicando o equilíbrio de energia para a bomba 1, então teremos:
Agora, da mesma forma, para a bomba 2, temos:
Com isso, podemos descobrir o valor da entalpia no ponto 11 aplicando o equilíbrio de energia para a bomba 2, então teremos:
Agora, com todos esses valores, podemos aplicar o equilíbrio de energia para o aquecedor de água de alimentação, onde teremos então:
Nesse caso temos regime permanente, então , dessa forma a equação se torna:
E analisando o regenerador fechado, teremos:
E, com a relação mássica para o regenerador fechado, a equação se torna:
Substituindo os valores conhecidos, temos:
Com esse valor, podemos encontrar a vazão mássica extraído da turbina para o aquecedor de água de alimentação, já que o enunciado nos deus a vazão que entra na turbina de 15 kg/s, então, teremos:
Passo 3
Agora, para encontrar a potência líquida e responder a letra (c), precisamos encontrar o calor que entra na caldeira e o calor que sai do condensador, dessa forma, começando pela caldeira, aplicando o equilíbrio de energia específica para ela, temos:
Substituindo os valores conhecidos, temos:
E, aplicando o equilíbrio de energia ao condensador:
Substituindo os valores conhecidos, temos:
Então, o trabalho líquido produzido pelo sistema será:
Passo 4
E, agora, usando também os calores que entram e saem do sistema encontrados no passo 3, podemos encontrar a eficiência do sistema através de:
Então, substituindo os valores conhecidos, temos: