Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 13.Problemas - Ex. 4
Considere a derivada na região bifásica (veja as Figs. 3.18 e 3.19) Qual é o significado de ? e o de ?
Passo 1
Salve gente, tudo bem? Então, a questão nos deu uma dica interessante. E tá nas figuras, vamo olhar essas figuras que a questão sugere, bele?
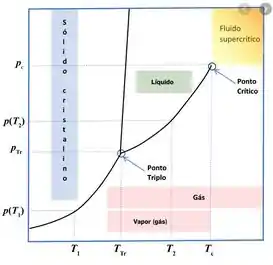
Observando esse gráfico da pressão de vapor, a gente observa justamente a região bifásica (ponto triplo, duas fases). Nessa fase, é uma função que depende somente de , logo, ela não depende de . V apenas compreende o volume, mas foge da equação de Clayperon nessa região bifásica.
Resposta
Exercícios de Livros Relacionados
Utilize a Equação 13.32 para obter uma expressão para ∂ T ∂ p s em função de T , v , c p e α p . Determine a variação de temperatura no processo onde água a 25 ° C e 100k P a é comprimida de moda isoe
O som se propaga no meio como ondas de pressão. Estas ondas podem ser modeladas como uma sequência de processos de compressão e expansão isoentrópica. A velocidade do som, c , é definida por c 2 = ∂ P
Desenvolva expressões para ∂ T ∂ v u e ∂ h ∂ s v que não contenham as propriedades h , u e s .
Determine a velocidade do som no ar a 20 ° C e 100k P a utilizando a Equação 13.43 e as relações politrópicas. Admita que o ar se comporte como um gás perfeito.
Utilize a relação de Gibbs d h = Td s + v d p e uma das relações de Maxwell para encontrar uma expressão para ∂ h ∂ v T que só envolva as propriedades p , v e T . Utilize seu resultado e a Equação 13.