Deseja-se comparar o desempenho de um refrigerador, com ciclo de absorção de amônia, com um refrigerador similar baseado no ciclo de compressão de vapor. Considere um sistema de absorção que apresenta temperatura no evaporador e no condensador, respectivamente, iguais a e . A temperatura no gerador deste sistema é e de calor são transferidos para a amônia, no evaporador, para cada transferido da fonte de alta temperatura, para a solução de amônia, no gerador. Para fazer a comparação pretendida, admita que seja disponível um reservatório para um motor reversível que rejeita o calor ao meio que está a . O trabalho produzido é então usado para acionar um sistema ideal de compressão de vapor que utiliza amônia como fluido refrigerante. Calcule a quantidade de refrigeração, que pode ser obtida por transferido do reservatório a alta temperatura, utilizando este arranjo com os que podem ser obtidos no ciclo de absorção.
Passo 1
FALA TU SOLDADO, DIREITA VOLVER, SENTIDO, simbora! Para essa questão precisaremos analisar os dois diagramas abaixo, que representam respectivamente, o processo que ocorre na máquina e o ciclo de refrigeração:
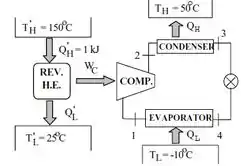
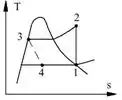
Com o diagrama do ciclo de refrigeração sabemos que, , logo, e ; . Estabelecido os dados que serão usados, se liga nas equações que estarão conosco nessa jornada:
(1)
(2)
(3)
(4)
(5)
(6)
DITO TUDO ISTO, podemos ir para a resolução do problema, acompanhe-me!
Passo 2
Primeiramente calcularemos a eficiência da máquina por meio da equação (1) e com os dados estabelecidos no diagrama:
Com isso podemos calcular o através da equação (2):
Agora vamos calcular o utilizando a equação (3):
Com a equação (4), calcularemos a taxa de transferência de calor do evaporador:
Com isso, podemos calcular o coeficiente de eficácia do ciclo pela equação (5):
Finalmente calcularemos a quantidade de refrigeração por meio da equação (6):
PRONTINHO, finalizamos tudo, até a próxima pessoal!