Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 2.Problemas - Ex. 38
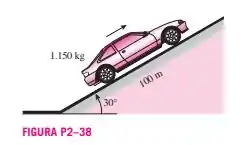
Determine a potência necessária para que um automóvel de 1.150 kg suba uma estrada em aclive de 100 m de comprimento com uma inclinação de 30° (com a horizontal) em 12 s a uma velocidade constante, do repouso a uma velocidade final de 30 m/s e de 35 m/s até uma velocidade final de 5 m/s. Despreze o atrito, o arrasto aerodinâmico e a resistência do rolamento.
Passo 1
Temos que, o automóvel está subindo uma estrada em aclive, nele estão presentes as energias cinética e potencial, assim, um trabalho será fornecido para que este automóvel realize sua trajetória. Como estamos tratando de potência, a potência nada mais é que a energia em trânsito por unidade de tempo, e, como estamos tratando de energia cinética e gravitacional, teremos:
Passo 2
Na alternativa , teremos que a potência derivada do trabalho da energia cinética será nula, pois como a velocidade é constante, a variação da velocidade será 0. Então ficaremos somente com a potência do trabalho da energia potencial.
Inicialmente, vamos calcular a diferença de altura entre a base da estrada e o topo, observe o esquema:
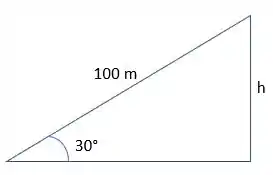
Temos que a altura será dada por:
Daí, calculando a potência do trabalho gravitacional, teremos:
Passo 3
Na letra , teremos a participação da potência do trabalho cinético pois, ele parte do repouso mas sua velocidade final é de 30 m/s, ou seja, existe uma diferença na velocidade. Assim, para calcularmos a potência do trabalho cinético, temos:
A potência do trabalho potencial será a mesma, pois a diferença de altura é a mesma, assim, a potência total necessária para o carro subir a estrada em aclive é:
Passo 4
Ao analisarmos a letra vemos que também teremos a potência do trabalho cinético, porém, o corpo ao invés de acelerar, está reduzindo sua velocidade, assim:
Como dito no passo anterior, a potência do trabalho gravitacional continua a mesma, pois a variação da altura é a mesma. Daí,
Resposta
;
;
;