Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 4.Problemas - Ex. 22
Durante um processo de expansão, a pressão de um gás muda de 15 para 100 psia de acordo com a relação , onde e é uma constante. Considerando que o volume inicial do gás é 7 pés³, calculo o trabalho realizado durante o processo.
Passo 1
Para resolver este problema, precisamos encontrar o volume no estado 2 (a 100 psia).
No estado 1, temos a seguinte relação:
Como , e são todos determinados no enunciado, conseguimos calcular o valor de b:
No estado 2, temos a seguinte relação:
Como já possuímos o valor de , podemos calcular o volume no estado final:
Passo 2
Note que possuímos uma função que relaciona pressão e volume, e que ela é uma reta. Podemos então plotar essa reta partindo do estado inicial até o final:
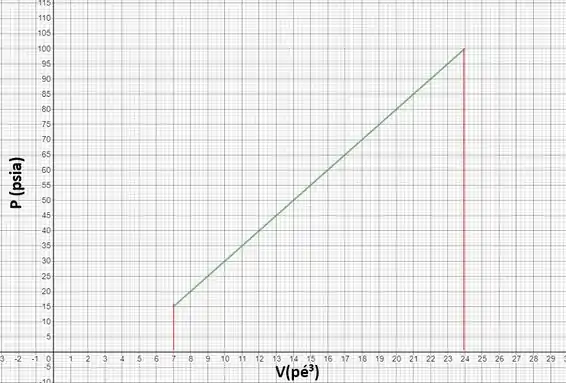
Devemos relembrar que o trabalho pode ser definido como:
Devemos lembrar também que o significado de uma integral é a área embaixo de uma curva.
Logo, para calcular o valor do trabalho de fronteira, devemos calcular a área da região limitada pela curva P-V e seus estados inicial e final.
Note que o nosso gráfico está delimitado em vermelho pelos estados inicial e final do processo. Assim é possível notar que a figura geométrica abaixo da curva é um trapézio. Devemos lembrar, então, a fórmula da área de um trapézio:
Ao comparar com o nosso gráfico, podemos notar que a base maior do trapézio se trata da pressão de 100 , enquanto a base menor trata-se da pressão de 15 e a altura é a variação de volume entre os estados 1 e 2. Assim:
Resposta
Para converter para Btu, basta lembrar que 1 Btu vale :
O sinal positivo indica que trabalho foi realizado pelo sistema.