Enunciado
Termodinâmica - Termodinamica,Teoria Cinética e Termodinâmica Estatística, Sears e Salinger- Ed: 3º - Capítulo 6.Problemas - Ex. 38
a) Esboce, em um diagrama , duas superfícies de entropia constante para um gás ideal, que obedece a lei de Curie.
b) Usando as duas superfícies da parte (a) juntamente com duas superfícies isotérmicas, esboce dois ciclos de Carnot possíveis para este sistema.
c) deduza a relação entre para processos em que sejam tanto isotermicos quanto isentrópicos. Esboce o processo no plano .
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão do livro de termodinâmica de Sears e Salinger ele deseja determinar:
a) Esboce, em um diagrama , duas superfícies de entropia constante para um gás ideal, que obedece a lei de Curie.
b) Usando as duas superfícies da parte (a) juntamente com duas superfícies isotérmicas, esboce dois ciclos de Carnot possíveis para este sistema.
c) deduza a relação entre para processos em que sejam tanto isotermicos quanto isentrópicos. Esboce o processo no plano .
Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Então galerinha ele deseja determinar os itens abaixo com base na superfície de entropia, com isso
Na letra (a) expressando o gráfico da entropia constante para um gás ideal que obedece a lei de Curie fica,
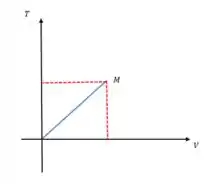
Já na letra (b) usando a superfície do gráfico acima temos que,
Ficando sua representação gráfica como,
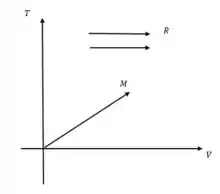
E por fim na letra determinar os termos para o processo isotérmico ficando,
Unificando a representação dada temos,
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.
Resposta
a) gráfico demonstrado no passo anterior.
b) gráfico demonstrado no passo anterior.
c)