Enunciado
Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 11.Problemas - Ex. 51
Ar escoa em um motor a gasolina a e . Ele é então comprimido em uma razão de compressão volumétrica de 8:1. O processo de combustão libera de energia com a queima do combustível. Determine a temperatura e a pressão após a combustão.
Passo 1
Fala, galera! Vamos resolver essa questão.
Vamos começar dando uma olhada no diagrama do processo:
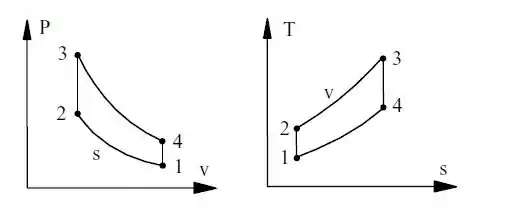
Vamos determinar a temperatura e a pressão no final de cada processo.
No processo de compressão isentrópica (), de 1 para 2, temos:
Usando a relação de compressão e os demais dados do enunciado, temos:
Para a pressão, vamos usar a mesa lógica:
Passo 2
No processo de combustão, de 2 a 3, temos um volume constante e a relação entre as energias internas:
Então, vamos determinar a temperatura e a pressão no final desse processo, como a questão pede:
E a pressão:
E concluímos o exercício. Valeu, galera! 😉