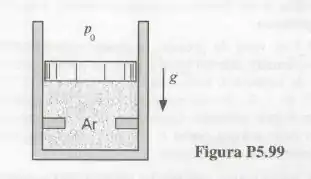
A Fig. 5.99 mostra um conjunto cilindro-pistão com esbarro. O conjunto contém de ar que, inicialmente, apresenta temperatura e pressão iguais a e . A atmosfera atua sobre o pistão e este tem massa não desprezível. O volume da câmara fica igual a quando ocorre o contato do pistão com o esbarro. O ar transfere calor para o ambiente a temperatura atinge . Determine o volume ocupado pelo ar e a pressão interna no estado final deste processo. Calcule, também, a transferência de calor e o trabalho realizado neste processo.

Olhando o diagrama fica tranquilo de determinar o trabalho, pois, o trabalho se da pela área integrável sobe a função no diagrama.

Temos outra forma de calcular é de que quando a pressão é constante temos que é nosso trabalho.

Calculando o trabalho:

Note que não temos calculado o nosso volume inicial.

Para determinar o volume inicial vamos considerar o ar um gás ideal, com isto, aplicando a fórmula do gás ideal:

Olhando na tabela , temos e substituindo valores:

Com volume inicial calculado, partiu calcular o trabalho:

Substituindo valores:

Calculando o calor transferido.

Aplicando a equação da energia, fica:

Como estamos considerando o ar um gás ideal, vamos olhar na tabela temos que a energia interna é:

Para :

Para :

Substituindo todas as variáveis no cálculo do calor, temos:

É isso galera valeu.