Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 113
A ideia de usar turbinas a gás para veículos automotores foi concebida na década de . Grandes fabricantes de automóveis fizeram considerável pesquisa nos anos e para desenvolver turbinas a gás automotivas, como as empresas Chrysler e Ford, nos Estados Unidos, e Rover, no Reino Unido. O primeiro automóvel do mundo de turbinas a gás, o de , foi construído em no Reino Unido, seguido pela produção do Plymouth Sport Coupe pela Chrysler em , sob a liderança de G.J. Huebner. Centenas de carros Plymouth movidos a turbina a gás foram construídos na década de para fins de demonstração, emprestados a um grupo seleto de pessoas para que se reunissem experiências de campo. Os usuários não tinham reclamações, além da lenta aceleração. Mas os carros nunca foram produzidos em massa por causa dos altos custos de produção (especialmente material) e a incapacidade de satisfazer as disposições da lei do ar limpo (Clear Air Act) de .
Uma turbina a gás do carro Plymouth, construída em 1960, tinha uma temperatura de entrada na turbina de , uma razão de pressão igual a e uma efetividade do regenerador igual a . Considerando eficiências isentrópicas de para o compressor e a turbina, determine a eficiência térmica do carro. Determine também a vazão mássica de ar para uma produção de potência líquida de 95 hp. Considere que o ar ambiente esteja a e .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O ciclo Brayton real com regeneração é dado por:
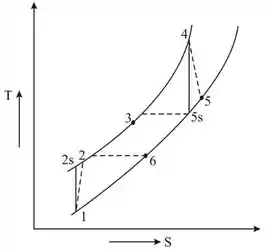
Do enunciado, temos que:
Analisando a tabela das propriedades do gás ideal, temos que para a temperatura , temos que:
Analisando o processo , temos que:
Portanto:
Passo 2
A partir da pressão relativa , podemos interpolar a entalpia correspondente a partir da tabela:
Podemos encontrar a entalpia real no estado a partir da eficiência isentrópica do compressor:
Passo 3
Analisando a tabela das propriedades do gás ideal, temos que para a temperatura , temos que:
E:
Analisando o processo , temos que:
Portanto:
Passo 4
A partir da pressão relativa , podemos interpolar a entalpia correspondente a partir da tabela:
Podemos encontrar a entalpia real no estado a partir da eficiência isentrópica da turbina:
Passo 5
Sabemos que a eficácia do regenerador é dada por:
Substituindo os valores, temos que:
O trabalho líquido é dado por:
Substituindo os valores, temos que:
O calor fornecido é dado por:
Passo 6
A eficiência térmica é dada por:
Ou:
A potência desenvolvida será:
Substituindo os valores, temos que: