Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 101
Uma usina de potência com turbina a gás opera em um ciclo Brayton simples entre os limites de pressão de e . O ar entra no compressor a e sai a a uma vazão mássica de . A temperatura máxima do ciclo é de. Durante a operação do ciclo, a produção de potência líquida é medida experimentalmente, e obtém-se como resultado . Considere as propriedades constantes para o ar a , com , , , .
(a) Represente graficamente o diagrama para o ciclo.
(b) Determine a eficiência isentrópica da turbina para essas condições de funcionamento.
(c) Determine a eficiência térmica do ciclo.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Bom... Para esboçar o nosso ciclo em um diagrama , temos que saber primeiramente se os processos de compressão e expansão serão totalmente isentrópicos ou não.
Como no item “b” pede-se a eficiência isentrópica da turbina, vamos considerar que o compressor é ideal () e que a turbina seja real (). Ou seja, teremos o estado ideal e o estado real.
O exercício nos disse que o ciclo opera entre as pressões de e . Sabemos que a baixa pressão ocorre no processo e a pressão maior no processo . Portanto:
Como o ar entra no compressor a e sai a , temos que:
Sabemos também que:
A temperatura máxima do ciclo é de. A maior temperatura em um ciclo Brayton ocorre na entrada da turbina (estado ), portanto:
Sabendo estes dados, temos que seu diagrama é dado por:
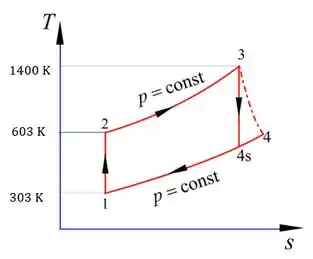
Passo 2
Para descobrir a eficiência isentrópica da turbina precisaremos saber as propriedades dos estados e .
O processo é uma expansão isentrópica, logo:
Temos que:
Substituindo os valores temos que:
Passo 3
Temos que o trabalho de turbina isentrópico é de:
Substituindo os valores, temos que:
Para o trabalho isentrópico do compressor, temos que:
Substituindo os valores, temos que:
Também podemos encontrar um trabalho real para a turbina de acordo com a seguinte equação:
Logo:
Passo 4
A eficiência isentrópica da turbina será então:
Substituindo os valores, temos que:
A eficiência térmica é dada por:
Portanto, a eficiência térmica será:
Ou: