Inicialmente, um conjunto cilindro-pistão-mola linear contém de ar a e . O ar é então aquecido, num processo onde a relação entre a pressão e o volume é linear, até o estado onde o volume interno da câmara se torna igual ao dobro do volume inicial. Faça um gráfico desse processo num diagrama . Determine, também, o trabalho e o calor transferido no processo.

Galera como o processo é uma expansão, logo, o ar esta aumentando seu volume isso significa que a pressão interna dele está aumentando, portanto, o diagrama fica:

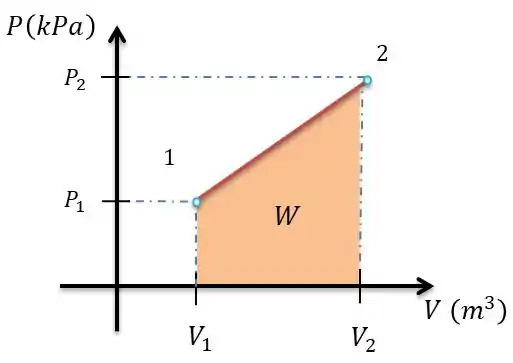
E para calcular o trabalho do nosso processo ele será igual à área sobe a reta do nosso diagrama.

Temos a área de um trapézio.

Para conseguirmos calcular o trabalho final temos que calcular o volume inicial e a pressão final.

Calculando o volume inicial.

Considerando o ar como gás ideal podemos aplicar a fórmula do gás ideal.

Olhando na tabela o é , convertendo e substituindo valores na fórmula, fica:

Para calcular a pressão final teremos que utilizar do artifício dito no enunciado.

Utilizando a equação do gás ideal.

Relação entre a pressão e o volume é linear, isso significa que:

Como

Galera aqui o enunciado do livro não está fornecendo um dado que deveria ser dito que é o valor final da temperatura, sem este dado não é possível calcular os quesitos que ele mesmo pede, portanto, utilizaremos o valor de .

Com o volume e pressão calculados vamos determinar o trabalho realizado.

Substituindo valores, temos:

Escrevendo a equação do calor transferido:

Como estamos considerando o ar um gás ideal, vamos olhar na tabela temos que a energia interna é:

Para :

Para :

Substituindo todas as variáveis no cálculo do calor, temos:

É isso galera, até a próxima.