Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 4.Problemas - Ex. 10

Uma massa de 5 kg de vapor de água saturado a 300 kPa é aquecida a uma pressão constante até que a temperatura atinja 200 °C. Calcule o trabalho realizado pelo vapor durante o processo.

Passo 1

A questão é sobre uma massa de água que se encontra em um estado inicial (estado 1) com pressão inicial P 1 e, após ser aquecida, ela sua pressão final P 2 permanece igual à pressão inicial P 1 . O enunciado do problema pede para encontrarmos o trabalho W realizado no aquecimento isobárico (a pressão constante) desses 5   k g de água. A figura abaixo ilustra o problema.

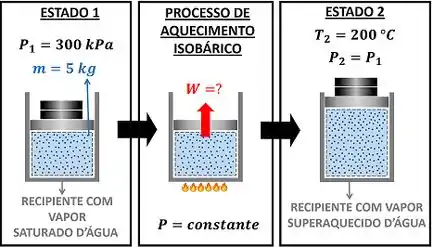
m é a massa de água presente no recipiente. Como o recipiente não perde nem ganha massa durante o processo de aquecimento, a massa m é constante.

m = c o n s t a n t e

T 2 é a temperatura final da água após o aquecimento.

Para achar quanto vale o trabalho W realizado pela água durante seu aquecimento, devemos primeiro encontrar os valores as propriedades da água nos estados inicial (estado1) e final (estado 2) a partir das suas tabelas termodinâmicas.

Faremos isso no próximo passo!

Passo 2

Nesse passo, vamos apenas usar as tabelas termodinâmicas da água. Só no passo seguinte que calcularemos W !

Primeiro, devemos encontrar o valor do volume específico v 1 da água de quando ela se encontra no estado 1 (vapor saturado a 300   k P a ). Consultando a Tabela A-5 (página 916) para água como líquido-vapor saturado, podemos encontrar o volume específico em uma condição de vapor saturado para uma pressão de 300   k P a :

P 1 =   300   k P a c o n d i ç ã o   d e   v a p o r   s a t u r a d o     ⟹     ν 1 = ν v a p o r   s a t u r a d o   = 0,60582   m ³ / k g  

Consideramos agora o estado 2, onde a temperatura é de 200   ° C e a pressão continua a valer 300   k P a . Consultando novamente a Tabela A-5, vemos que para uma pressão de 300   k P a a temperatura de saturação da água é de 133,52 ° C . Como a temperatura final da água T 2 é maior do que a temperatura de saturação da água   T 2 > T s a t , então a água está num estado de vapor superaquecido.

T 2 > T s a t       ⟹       V a p o r   s u p e r a q u e c i d o   d ' á g u a

Isso quer dizer que, para achar as propriedades do estado 2, precisamos usar a tabela de vapor d’água superaquecido. A Tabela A-6 (página 918) apresenta as propriedades do vapor superaquecido d’água. Entrando com os valores de temperatura T 2 = 200   ° C e pressão P 2 = 300   k P a nessa tabela, podemos encontrar o valor do volume específico v 2 da água após seu aquecimento.

P 2 =   300   k P a T 2 =   200   ° C     ⟹     ν 2 = 0,71643   m ³ / k g  

Passo 3

O trabalho W que a água realiza é um trabalho de expansão de fronteira, porque ela empurra o ambiente para ocupar um espaço maior. Além disso, o processo de expansão é um processo a pressão constante (processo isobárico). Logo, para resolver o problema, devemos lembrar da equação para calcular o trabalho de fronteira de um processo a pressão constante.

W =   m ⋅ ∫ 1 2 P d v       ⟹       W = m ⋅ P ⋅ ( ν 2 - ν 1 )

Vemos pela equação acima que, como a pressão P é constante P = 300   k P a , ela pode sair da integral! Isso deixa a equação muito mais simples de ser usada!

Substituindo os dados nessa equação, achamos:

W = m ⋅ P ⋅ ν 2 - ν 1

W = 5 ⋅ 300 ⋅ 0,71643 - 0,60582

W = 165,9   k J

Resposta

W = 165,9   k J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma determinada massa de ar com n = 1,5 inicialmente a 2 Mpa e 300 °C é expandida em um processo politrópico para 80 kPa em um arranjo pistão-cilindro. Determine a temperatura final do ar.
Obtenha uma expressão geral para o trabalho produzido por um gás ideal quando ele passa por um processo politrópico em um sistema fechado do estado inicial 1 ao estado final 2. Para o resultado, deve-
Uma massa de 5 kg de uma mistura de água líquida e vapor de água saturados está contida em um arranjo pistão-cilindro a 125 kPa. Inicialmente, dois quilos de água estão na fase líquida e o restante na
Um arranjo pistão-cilindro sem atrito contém inicialmente ar a 100 kPa e 0,15 m³. Nesse estado, uma mola linear ( F ∝ x ) está tocando o pista, mas sem exercer qualquer força sobre o mesmo. O ar é ent
Hélio inicialmente a 1.500k P a e 300° C e expandido em uma turbina ate 100k P a e25° C . Determine o trabalho máximo que essa turbina pode produzir, em k J / k g . O trabalho maximo exige uma turbina