Enunciado

Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 7.Problemas - Ex. 62

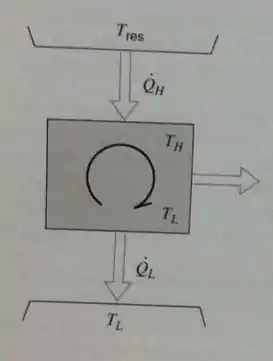
Um motor térmico de Carnot, mostrado na Fig. P7.62, recebe energia de um reservatório a através de um trocador de calor, onde o calor transferido é proporcional à diferença de temperatura e dado por . O motor rejeita calor a uma temperatura dada, . Para projetar o motor térmico de modo a obter a potência máxima de saída, mostre que o reservatório a alta temperatura, , no ciclo deve ser selecionado com .

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Bem, o trabalho pode ser dado da seguinte maneira:

Expandindo os termos

Para encontrar o valor máximo de , nós devemos igualar a derivada a zero, com isso, temos o seguinte equacionamento

Logo, essa derivada será igual a

Fazendo algumas manipulações,

Resposta

Exercícios de Livros Relacionados

Dois combustíveis diferentes podem ser usados em um motor térmico operando entre a temperatura de combustão do combustível e uma fonte de baixa temperatura a 350K . O combustível A queima a 2200K , li

Uma casa é mantida aquecida, a T H , por uma bomba de calor acionada por um motor elétrico usando o meio exterior como reservatório a baixa temperatura, T L . As perdas de energia da casa são diretame

Uma fornalha pode fornecer calor, Q H 1 a T H 1 para ser usado por um motor térmico com rejeição de calor a T a t m , conforme mostrado na Fig. P7.59. O motor térmico aciona uma bomba de calor que lib

Um refrigerador, mantendo 5 ° C em seu interior, está localizado em um ambiente a 30 ° C . O refrigerador deve ter uma temperatura alta Δ T graus acima da temperatura ambiente e uma temperatura baixa