Um motor de turbina a gás funciona segundo um ciclo Brayton ideal com regeneração, como mostrado na . O regenerador é então rearranjado para que as correntes de ar dos estados entrem em uma extremidade do regenerador e as correntessaiam na outra extremidade (isto é, o arranjo de fluxo paralelo de um trocador de calor). Considere tal sistema quando ar entra no compressor a ; a razão de pressão do compressor é igual a ; a temperatura máxima do ciclo é de ; e a diferença entre as temperaturas das correntes de ar quente e frio é de no final do regenerador, onde o fluxo frio deixa o regenerador. O arranjo do ciclo mostrado na figura é mais ou menos eficiente do que esse arranjo? Considere que o compressor e a turbina são isentrópicos. Trabalhe com calores específicos constantes à temperatura ambiente.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Bom... Para esboçar o nosso ciclo em um diagrama , temos que saber primeiramente se os processos de compressão e expansão serão totalmente isentrópicos ou não.
No caso os processos são totalmente isentrópicos.
O exercício nos disse que o ciclo opera com e que a pressão na entrada do compressor é de . Sabemos que a baixa pressão ocorre no processo e a pressão maior no processo . Portanto:
Como o ar entra no compressor a , temos que:
Sabemos também que:
A temperatura máxima do ciclo é de. A maior temperatura em um ciclo Brayton ocorre na entrada da turbina (estado ), portanto:
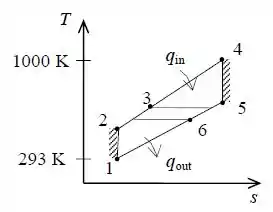
Sabendo estes dados, temos que seu diagrama é dado por:
Passo 2
Agora vamos analisar os processos:
O processo é uma compressão isentrópica, logo:
Temos que:
Logo:
Substituindo os valores temos que:
Passo 3
Para a expansão , temos que:
Como:
Substituindo os valores, temos que:
Sabendo que o ar quente na entrada do regenerador (trocador de calor) é representado pelo estado e o ar frio na saída do mesmo é representado pelo estado , e que a corrente de ar frio sai do regenerador mais fria do que a corrente de ar quente na sua entrada, temos que:
Convertendo a temperatura do estado para , temos que:
Ou:
Passo 4
Fazendo o balanço energético no regenerador, temos que:
Substituindo os valores, temos que:
Passo 5
A eficiência térmica será:
Passo 6
foi a eficiência encontrada para o arranjo da figura. Se fizermos o arranjo do enunciado, temos a seguinte condição:
Fazendo o balanço de energia novamente, temos que:
Resolvendo o sistema de equações, temos que:
E:
Passo 7
A eficiência térmica do segundo arranjo será:
Portanto, é possível dizer que o arranjo do ciclo da é mais eficiente.
Resposta
O arranjo do ciclo da é mais eficiente.