Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 182

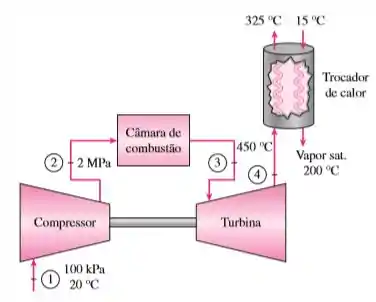
As necessidades de eletricidade e calor do processo de uma instalação fabril devem ser atendidas por uma usina de cogeração formada por uma turbina a gás e um trocador de calor para produção de vapor de água. A usina opera no ciclo Brayton simples entre os limites de pressão de 100 kPa e 1.000 kPa, utilizando o ar como fluido de trabalho. O ar entra no compressor a 20 °C. Os gases de combustão saem da turbina e entram no trocador de calor a 450 °C, saindo dele a 325 °C, enquanto a água líquida entra no trocador de calor a 15 °C e sai a 200 °C como vapor saturado. A potência líquida produzida pelo ciclo de turbina a gás é de 1.500 kW. Considerando uma eficiência isentrópica do compressor de 86%, uma eficiência isentrópica da turbina de 88% e calores específicos variáveis, determine

  1. a vazão mássica de ar
  2. a razão de consumo de trabalho e a eficiência térmica
  3. a taxa na qual vapor de água é produzido no trocador de calor.

    4. Determine também

  4. a eficiência de utilização da planta de cogeração, definida como a razão entre energia total utilizada e a energia fornecida para a usina.

Passo 1

Vamos assumir que:

As premissas do padrão aéreo são aplicáveis.

As alterações cinéticas e potenciais de energia são insignificantes.

O ar é um gás ideal com aquecimentos específicos variáveis.

Passo 2

Para esse problema, usamos as propriedades do ar do software EES. Lembre-se de que, para um gás ideal, a entalpia é uma função da temperatura apenas enquanto a entropia é uma função da temperatura e da pressão.

Processo 1-2: Compactação

T 1 = 20   º C   → h 1 = 293.5   k J k g

P 1 = 100   k P a → s 1 = 5.682   k J k g . K

P 2 = 1000   k P a → h 2 s = 567.2   k J k g

s 2 = s 1 = 5.682   k J k g . K

η C = h 2 s - h 1 h 2 - h 1 → h 2 = 611.8   k J k g

Processo 3-4: Expansão

T 4 = 450   º C → h 4 = 738.5   k J k g

η T = h 3 - h 4 h 3 - h 4 s → 0.88 = h 3 - 738.5 h 3 - h 4 s

Não podemos encontrar a entalpia no estado 3 diretamente. No entanto, usando o seguinte código no EES, juntamente com a eficiência isentrópica, encontramos:

h 3 = 1262   k J k g ,   T 3 = 913.2   º C ,   s 3 = 6.507   k J k g . K

A solução manualmente exigiria uma abordagem de erro de teste.

Abaixo, o código:

h _ 3 = e n t h a l p y ( A i r ,   T = T _ 3 )

s _ 3 = e n t r o p y ( A i r ,   T = T _ 3 ,   P = P _ 1 ,   s = s _ 3 )

h _ 4 s = e n t h a l p y ( A i r ,   P = P _ 1 , s = s _ 3 )

Além disso, temos a temperatura:

T 5 = 325   º C → h 5 = 605.4   k J k g

Passo 3

A água de entrada é um líquido comprimido a 15ºC e à pressão de saturação do vapor a 200ºC (1555 kPa). Isso não está disponível nas tabelas, mas podemos obtê-lo no EES. A alternativa é usar entalpia líquida saturada à temperatura determinada.

T w 1 = 15 º C → h w 1 = 64.47   k J k g

P 1 = 1555   k P a

T w 2 = 200 º C → h w 2 = 2792   k J k g

x 2 = 1

A produção líquida de trabalho é:

w C , e n t = h 2 - h 1 = 318.2   k J k g

w T , s a í d a = h 3 - h 4 = 523.4   k J k g

w l í q = w T , s a í d a - w C , e n t = 205.2   k J k g

E a taxa de fluxo de massa do ar é:

m ˙ a = W ˙ l í q w l í q = 7.311   k g s

Passo 4

Para a letra b, a taxa de retrabalho é:

r b w = w C , e n t w T , s a í d a = 0.608

A taxa de entrada de calor e a eficiência térmica são:

Q ˙ e n t = m ˙ a ( h 3 - h 2 ) = 4753   k W

η t h = W ˙ l í q Q ˙ e n t = 31.6 %

Passo 5

Na letra c, um balanço energético no trocador de calor fornece:

m ˙ a ( h 4 - h 5 ) = m ˙ w ( h w 2 - h w 1 ) → m ˙ w = 0.3569   k g s

Passo 6

E por fim, na letra d, o calor fornecido à água no trocador de calor (calor do processo) e a eficiência de utilização são:

Q ˙ p = m ˙ w ( h w 2 - h w 1 ) = 973.5   k W

ϵ u = W ˙ l í q + Q ˙ p Q ˙ e n t = 52.0   %

Resposta

  1. m ˙ a = 7.311   k g s
  2. r b w = 0.608

    3. η t h = 31.6 %

  3. m ˙ w = 0.3569   k g s
  4. ϵ u = 52.0   %
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um motor a gasolina apresenta uma vazão de compressão volumétrica de 9:1. O estado antes da compressão é de 290K e 90k P a , e a temperatura de pico do ciclo é de 1800K . Determine a pressão após a ex
Repita o problema 11.37, mas considere que o compressor tem um rendimento isoentrópico de 85 % e a turbina um rendimento isoentrópico de 88 % .
Um motor a diesel apresenta um estado antes da compressão de 95k P a e 290K , um pico de pressão de 6000k P a , e uma temperatura máxima de 2400K . Determine a razão de compressão volumétrica e o rend
Resolva o problema precedente, mas use as propriedades da Tabela A.7 e não as propriedades do ar frio.
Um motor a diesel tem, antes da compressão, ar a 280K e 85k P a . A maior temperatura é de 2200K e a maior pressão é de 6M P a . Determine a razão de compressão volumétrica e a pressão média efetiva,