Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 12.Problemas - Ex. 78

Oxigênio a 200   p s i a e 600   ° F é expandido adiabaticamente e reversivelmente em um bocal para 70   p s i a . Determine a velocidade na qual o oxigênio sai do bocal, considerando que ele entra com velocidade desprezível. Trate o oxigênio como um gás ideal com calores específicos variáveis com a temperatura. Utilize os diagramas de desvio.

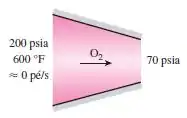
Passo 1

Pessoal, as propriedades do oxigênio podem ser extraídas na tabela A - 1 , no apêndice do livro:

M = 31,999   l b m / l b m o l ; R = 0 , 06206 B t u l b m ⋅ R ; T c r = 278,6   R ; P c r = 736   p s i a

A temperatura na saída deve ser determinada pelo fato de que o processo é isentrópico e a variação da entropia molar entre a entrada e saída é zero. Da equação da variação da entropia para um gás ideal, temos:

s - 2 - s - 1 i d e a l = 0

s ˙ 2 - s ˙ 1 = R u ln ⁡ P 2 P 1 = 1,9858 ln ⁡ 70 200 = - 2,085 B t u l b m o l ⋅ R

Assim, da tabela do livro A - 19 E ,

T 1 = 1060   R   →     h - 1 , i d e a l = 7543,6 B t u l b m o l   ;   s ˙ 1 = 53,921 B t u l b m o l ⋅ R

s ˙ 2 = s ˙ 1 - 2,085 = 53,921 - 2085 = 51,836 B t u l b m o l ⋅ R

s ˙ 2 = 51,836 B t u l b m o l ⋅ R   →     T 2 = 802   R ;   h - 2 , i d e a l = 5614,1 B t u l b m o l    

A variação da entalpia por mol é:

h - 2 - h - 1 i d e a l = h - 2 , i d e a l - h - 1 , i d e a l = 5614,1 - 7543,6 = - 1929,5   B t u / l b m o l

A mudança de entalpia por massa é:

h 2 - h 1 i d e a l = h - 2 - h - 1 i d e a l M = - - 1929,5 31,999 = - 60,30 B t u l b m

O balanço de energia no bocal é igual a:

E ˙ e n t = E ˙ s a i d a

m ˙ h 1 + V 1 2 2 = m ˙ h 2 + V 2 2 2

h 1 + V 1 2 2 = h 2 + V 2 2 2

Encontrando o valor de V 2 , temos:

V 2 = V 1 2 + 2 h 1 - h 2 1 2

V 2 = 0 2 + 2 60,30 25037 1 / 2 = 1738   p é s / s  

Passo 2

Os desvios de entalpia do oxigênio nos estados especificados são determinados a partir dos diagramas generalizados (Figuras A-29):

T R 1 = T 1 T c r = 106 0 278,6 = 3,805

p R 1 = p 1 p c r = 200 736 = 0,272

Z h 1 = 0 , 000759

E,

T R 2 = T 2 T c r = 802 278,6 = 2,879

p R 2 = p 2 p c r = 7 0 736 = 0 , 0951

Z h 2 = 0 , 00894

Portanto, podemos calcular a variação da entalpia:

h 2 - h 1 = h 2 - h 1 i d e a l - R u T c r Z h 2 - Z h 1

h 2 - h 1 = - 60,30 - ( 0,06206 ) ( 278,6   R ) ( 0,00894 - 0,000759 )

h 2 - h 1 = - 6044   B t u / l b m

A velocidade de saída será:

V 2 = V 1 2 + 2 h 1 - h 2 1 2

V 2 = 0 2 + 2 60 , 44 25037 1 / 2 = 17 40   p é s / s  

Resposta

As velocidades são:

V 2 = 1738   p é s / s

V 2 = 1740   p é s / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Pelo mesmo método usado no problema anterior, mostre que se a função de Gibbs deve decrescer durante qualquer processo espontâneo em que a temperatura e a pressão permanecem constantes,a) a função de
Uma turbina a vapor recebe um fluxo de vapor de 5000k g h - 1 , e seu rendimento é de 500 quilowatts. Despreze qualquer perda de calor da turbina. Encontre a variação na entalpia especifica do vapor q
Mostre que:a) ∂ h ∂ P T = - μ c p b) ∂ h ∂ T v = c p 1 - β μ k c) ∂ h ∂ v T = μ c p v k d) ∂ T ∂ v h = μ ( v k - μ v β )
As figuras 2.16 ,2.17 , 3.10e( 3.11 ) fornecem dados sobre o cobre e o mercúrio. Estes dados são suficientes para determinar todas as propriedades do cobre e do mercúrio entre 500K e 1000K ? Se for as
Para uma substância paramagnética, o trabalho específico em um processo reversível é - H d m . a) considere que o estado da substância seja definido pelo momento magnético por unidade de volume m e al