Qual processo do ciclo no Prob. 11–123 tem a maior taxa de destruição de exergia quando o reservatório de baixa temperatura está a 18 °C e o reservatório de alta temperatura está a 25 °C?
Passo 1
Oi pessoal, tudo bem?
Bem, para o problema, podemos esboçar o diagrama T-s como:
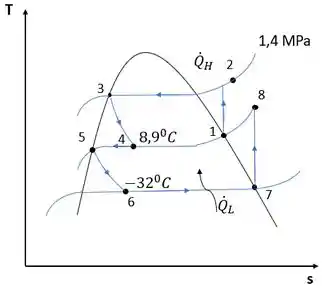
Bem, para este caso, devemos encontrar os valores respectivos das entropias, uma vez que o problema pede a destruição da exergia.
Passo 2
Assim, sabemos que o estado 1 se encontra em vapor saturado e possui e sabendo que o refrigerante é o R-134a, da tabela termodinâmica de vapor saturado:
Sabe-se que o estado 2 se encontra em vapor superaquecido com e que , então: .
O estado 3 está em líquido saturado e possui , então:
E assumindo que há estrangulamento de 3-4, temos
Uma vez que os estados 4 e 6 estão em mistura, e que e , devemos encontrar os seus respectivos títulos para posterior entropias, então podemos iniciar com:
Então:
O estado 5 está em líquido saturado e , então:
E assumindo que há estrangulamento de 5-6, temos
E
Então:
O estado 7 encontra-se em vapor saturado e , então:
Sabendo que , e analisando das tabelas termodinâmicas que a pressão de saturação para a temperatura de é , temos:
Passo 3
A destruição da exergia durante um processo de fluxo de um estado de entrada para o estado de saída é dado por:
Portanto, aplicando a fórmula em cada componente do ciclo, temos:
Obs: e ;
Obs: e
E por fim:
Note que as vazões mássicas não foram informadas nesta questão, pois já foram encontradas no problema 11-123. Portanto, devemos rever o problema anterior para o entendimento das vazões mássicas.
Resposta
Portanto a maior taxa de destruição de exergia ocorre na fase de condensação em que .