Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 10.Problemas - Ex. 51
Reconsidere o Prob. 10-49E. Usando o EES (ou outro programa), determine a pressão ótima de extração para o aquecedor de água de alimentação aberto que maximiza a eficiência térmica do ciclo.
Passo 1
Para nos ajudar a visualizar o problema, vamos utilizar o diagrama do ciclo Rankine com regenerador aberto fornecido nessa seção do livro:
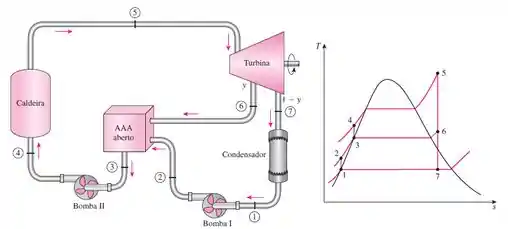
Primeiro temos que converter os dados fornecidos para podermos obter os dados nas tabelas termodinâmicas:
Temos ainda algumas outras condições, como:
Dessa forma, vamos jogar esses valores no EES para obter as propriedades termodinâmicas nesses estados, juntamente com as equações de equilíbrio de energia.
Passo 2
Dessa forma, o código para a resolução do exercício será:
P[5]=3447,4 [kPa]
T[5]=315,5 [C]
P[6]=275,8 [kPa]
P[7]=34,5 [kPa]
x[3]=0
"Análise da bomba 1 "
P[1]=P[7]
x[1]=0
h[1]=enthalpy(STEAM; P=P[1]; x=x[1])
v[1]=volume(STEAM; P=P[1]; x=x[1])
P[3]=P[6]
P[2]=P[3]
w_b_1=v[1]*(P[2]-P[1])
h[2]=h[1]+w_b_1
"Análise da bomba 2"
h[3]=enthalpy(STEAM; P=P[3]; x=x[3])
v[3]=volume(STEAM; P=P[3]; x=x[3])
P[4]=P[5]
w_b_2=v[3]*(P[4]-P[3])
h[4]=h[3]+w_b_2
"Análise da turbina"
h[5]=enthalpy(STEAM; P=P[5]; T=T[5])
s[5]=entropy(STEAM; P=P[5]; T=T[5])
s[6]=s[5]
h[6]=enthalpy(STEAM; P=P[6]; s=s[6])
x[6]=quality(STEAM; P=P[6]; s=s[6])
s[7]=s[5]
h[7]=enthalpy(STEAM; P=P[7]; s=s[7])
x[7]=quality(STEAM; P=P[7]; s=s[7])
"Análise do regenerador"
y*h[6]+(1-y)*h[2]=h[3]
"Análise da caldeira"
q_e=h[5]-h[4]
"Análise do condensador"
q_s=(1-y)*(h[7]-h[1])
"Eficiência do sistema"
Eta=1-q_s/q_e
Passo 3
A tabela paramétrica gerada é dada a seguir:
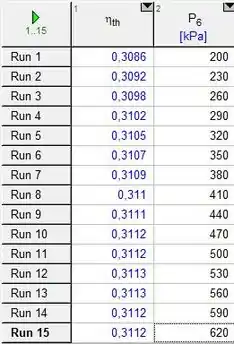
E o gráfico da eficiência pela pressão será:
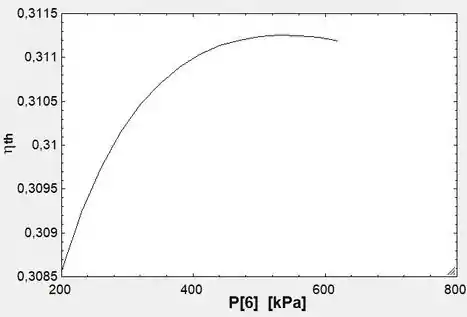
Com isso, podemos observar que a eficiência ótima ocorre para