Reconsidere o Prob. 10-53. Usando o EES (ou outro programa), determine a quantidade de calor adicional que deve ser fornecida para a caldeira quando a eficiência isentrópica da turbina, antes e depois do ponto de extração, estiver a 90% e houver uma queda de pressão de 10 kPa através da caldeira.
Passo 1
Tá legal, vamos começar o exercício escrevendo o código para resolver o problema, com todas as análises de volume de controle separadas, então, teremos:
"Dados do problema"
P[3]=3000 [kPa]
DELTAP_caldeira=10 [kPa]
P[4]=P[3]-DELTAP_caldeira
T[4]=350 [C]
P[5]=1000 [kPa]
P[6]=20 [kPa]
eta_T=0,90
P[2]=P[3]
P[7]=P[5]
P[1]=P[6]
"Análise da bomba"
x[1]=0
h[1]=enthalpy(STEAM; P=P[1]; x=x[1])
v[1]=volume(STEAM; P=P[1]; x=x[1])
w_b=v[1]*(P[2]-P[1])
h[2]=h[1]+w_b
"Análise da turbina"
h[4]=enthalpy(STEAM; P=P[4]; T=T[4])
s[4]=entropy(STEAM; P=P[4]; T=T[4])
s[5]=s[4]
h_s[5]=enthalpy(STEAM; P=P[5]; s=s[5])
T[5]=temperature(STEAM; P=P[5]; s=s[5])
x_s[5]=quality(STEAM; P=P[5]; s=s[5])
s[6]=s[4]
h_s[6]=enthalpy(STEAM; P=P[6]; s=s[6])
x_s[6]=quality(STEAM; P=P[6]; s=s[6])
h[5]=h[4]-eta_T*(h[4]-h_s[5])
h[6]=h[4]-eta_T*(h[4]-h_s[6])
x[5]=quality(STEAM; P=P[5]; h=h[5])
x[6]=quality(STEAM; P=P[6]; h=h[6])
"Análise do regenerador"
x[7]=0
h[7]=enthalpy(STEAM; P=P[7]; x=x[7])
T[7]=temperature(STEAM; P=P[7]; x=x[7])
T[3]=T[7]
h[3]=enthalpy(STEAM; P=P[3]; T=T[3])
y=(h[3]-h[2])/(h[5]-h[7])
"Análise da caldeira"
q_e=h[4]-h[3]
"Análise da turbina"
w_T=h[4]-h[5]+(1-y)*(h[5]-h[6])
"Eficiência térmica do ciclo"
w_liq=w_T-w_b
Eta_th=w_liq/q_e
Passo 2
Dessa forma, rodando o código, temos os seguintes resultados:
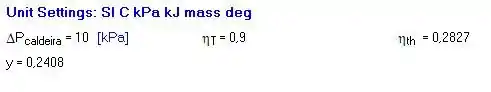

Então, o calor que deve ser adicionado na caldeira será: