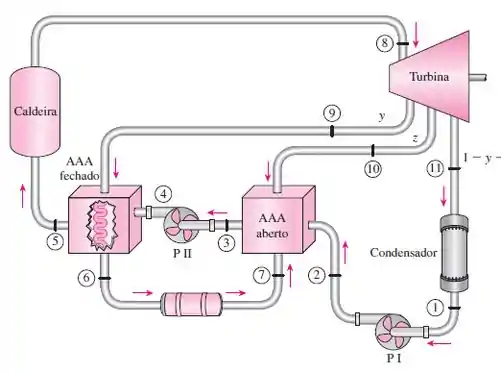
Reconsidere o Prob. 10-58. Usando o EES (ou outro programa), investigue os efeitos das eficiências da turbina e da bomba sobre o fluxo de massa e a eficiência térmica, considerando uma variação de 70 a 100% nessas eficiências. Trace curvas para o fluxo de massa e para a eficiência térmica como função da eficiência da turbina para eficiências da bomba de 70%, 85% e 100%, e discuta os resultados em seguida. Desenhe também o diagrama T-s para uma eficiência da turbina e da bomba igual a 85%.
Passo 1
A primeira coisa nesse exercício é retornar ao exercício 10.58 e verificar as considerações feitas para se encontrar as propriedades, o código escrito no EES posssui as mesmas considerações. Tá legal, então o código do EES que contém todas as variáveis e equações utilizadas na resolução do problema está descrito a seguir:
"Dados fornecidos pelo enunciado"
P[8] = 10000 [kPa]
T[8] = 600 [C]
P[9] = 1200 [kPa]
P_reg_fech=600 [kPa]
P[10] = P_reg_fech
P_cond=10 [kPa]
P[11] = P_cond
W_dot_liq=400000 [kW]
"Eta_turb= 100/100" "Eficiência isentrópica da turbina"
Eta_turb_hp = Eta_turb "Eficiência isentrópica para alta pressão"
Eta_turb_ip = Eta_turb "Eficiência isentrópica para média pressão"
Eta_turb_lp = Eta_turb "Eficiência isentrópica para baixa pressão"
Eta_bomba = 100/100 "Eficiência isentrópica da bomba"
"Análise da bomba 1"
P[1] = P[11]
P[2]=P[10]
h[1]=enthalpy(STEAM; P=P[1]; x=0)
v1=volume(STEAM; P=P[1]; x=0)
s[1]=entropy(STEAM; P=P[1]; x=0)
T[1]=temperature(STEAM; P=P[1]; x=0)
w_b_1_s=v1*(P[2]-P[1])
w_b_1=w_b_1_s/Eta_bomba "Eficiência da bomba 1"
h[1]+w_b_1= h[2]
s[2]=entropy(STEAM; P=P[2]; h=h[2])
T[2]=temperature(STEAM; P=P[2]; h=h[2])
"Análise do regenerador aberto"
z*h[10] + y*h[7] + (1-y-z)*h[2] = 1*h[3]
h[3]=enthalpy(STEAM; P=P[3]; x=0)
T[3]=temperature(STEAM; P=P[3]; x=0)
s[3]=entropy(STEAM; P=P[3]; x=0)
"Análise da bomba 2"
P[5]=P[8]
P[4] = P[5]
P[3]=P[10]
v3=volume(STEAM; P=P[3]; x=0)
w_b_2_s=v3*(P[4]-P[3])
w_b_2=w_b_2_s/Eta_bomba "Eficiência da bomba 2"
h[3]+w_b_2= h[4]
s[4]=entropy(STEAM; P=P[4]; h=h[4])
T[4]=temperature(STEAM; P=P[4]; h=h[4])
"Análise regenerador fechado"
P[6]=P[9]
y*h[9] + 1*h[4] = 1*h[5] + y*h[6]
h[5]=enthalpy(STEAM; P=P[6]; x=0)
T[5]=temperature(STEAM; P=P[5]; h=h[5])
s[5]=entropy(STEAM; P=P[6]; h=h[5])
h[6]=enthalpy(STEAM; P=P[6]; x=0)
T[6]=temperature(STEAM; P=P[6]; x=0)
s[6]=entropy(STEAM; P=P[6]; x=0)
"Análise válvula de estrangulamento"
P[7] = P[10]
y*h[6] = y*h[7]
T[7]=temperature(STEAM; P=P[7]; h=h[7])
s[7]=entropy(STEAM; P=P[7]; h=h[7])
"Análise da caldeira"
q_e + h[5]=h[8]
h[8]=enthalpy(STEAM; T=T[8]; P=P[8])
s[8]=entropy(STEAM; T=T[8]; P=P[8])
"Análise da turbina"
ss[9]=s[8]
hs[9]=enthalpy(STEAM; s=ss[9]; P=P[9])
Ts[9]=temperature(STEAM; s=ss[9]; P=P[9])
h[9]=h[8]-Eta_turb_hp*(h[8]-hs[9]) "Eficiência isentrópica para turbina para alta pressão"
T[9]=temperature(STEAM; P=P[9]; h=h[9])
s[9]=entropy(STEAM; P=P[9]; h=h[9])
ss[10]=s[8]
hs[10]=enthalpy(STEAM; s=ss[10]; P=P[10])
Ts[10]=temperature(STEAM; s=ss[10]; P=P[10])
h[10]=h[9]-Eta_turb_ip*(h[9]-hs[10]) "Eficiência isentrópica para pressões intermediárias"
T[10]=temperature(STEAM; P=P[10]; h=h[10])
s[10]=entropy(STEAM; P=P[10]; h=h[10])
ss[11]=s[8]
hs[11]=enthalpy(STEAM; s=ss[11]; P=P[11])
Ts[11]=temperature(STEAM; s=ss[11]; P=P[11])
h[11]=h[10]-Eta_turb_lp*(h[10]-hs[11]) "Eficiência isentrópica para baixas pressões"
T[11]=temperature(STEAM; P=P[11]; h=h[11])
s[11]=entropy(STEAM; P=P[11]; h=h[11])
h[8] =y*h[9] + z*h[10] + (1-y-z)*h[11] + w_turb
"Análise do condensador"
(1-y-z)*h[11]=q_s+(1-y-z)*h[1]
"Eficiência do ciclo"
w_liq=w_turb - ((1-y-z)*w_b_1+ w_b_2)
Eta_th=w_liq/q_e
W_dot_liq = m_dot * w_liq
Passo 2
Então, rodando o programa em função da eficiência da turbina, obtemos a seguinte tabela paramétrica:
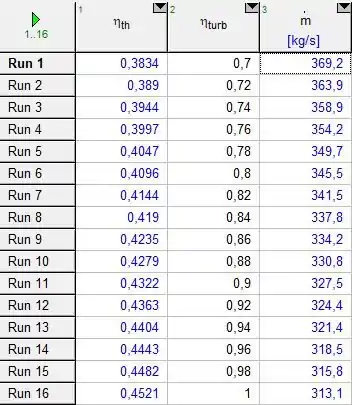
E, com essa tabela, conseguimos plotar o gráfico da eficiência da turbina pela eficiência térmica do ciclo:
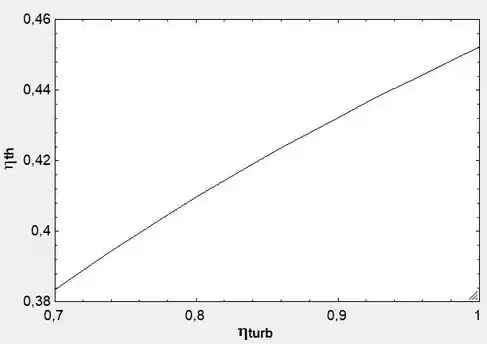
E, também, a eficiência da turbina pela vazão mássica do sistema:
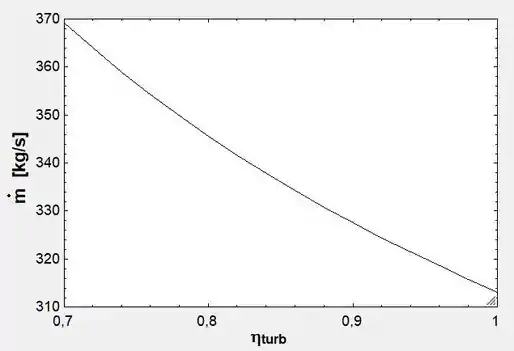
Passo 3
Agora, alterando a eficiência da turbina e da bomba para 85% no código do EES, podemos plotar o gráfico T-s dos estados a seguir:
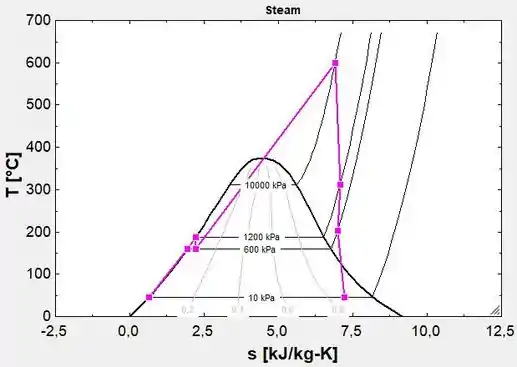
Resposta
Ei, a resposta está no passo a passo :)