Reconsidere o Prob. 10-83. Usando o EES (ou outro programa), estude os efeitos de uma variação de 10 a 20 na razão de pressão do ciclo a gás sobre a razão entre os fluxos de massa de ar e de vapor e sobre a eficiência térmica do ciclo. Mostre e discuta os resultados como funções da razão de pressões do ciclo a gás em um gráfico.
Passo 1
Tá legal, vamos primeiro ilustrar o diagrama T-s do ciclo gás-vapor com aquecedor de água de alimentação descrito no enunciado, então, temos:
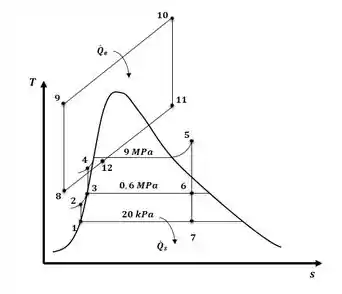
Agora, nós vamos basicamente repetir a análise feita no Problema 10-83, só que agora com o auxílio do EES, então, vamos passar todos os dados dos pontos conhecidos, e deixar com que ele encontre as propriedades de interesse pra nós. E depois, nós temos que escrever as equações de equilíbrio para os componentes, da mesma forma que fizemos no Problema anterior.
Passo 2
Sendo assim, o código do EES com comentários que resolve o problema em questão é dado a seguir:
"Dados fornecidos no enunciado"
T[8] = 300 [K]
P[8] = 14,7 [kPa]
"P_r = 14 Razão de pressão"
T[10] = 1400 [K]
T[12] = 460 [K]
P[12] = P[8]
W_dot_liq =450 [MW]
Eta_comp = 1
Eta_gas_turb = 1
Eta_bomba = 1
Eta_vapor_turb = 1
P[5] = 8000 [kPa]
T[5] =(400+273) [K]
P[6] = 600 [kPa]
P[7] = 20 [kPa]
"Análise do ciclo a gás"
"Análise do compressor"
s[8]=ENTROPY(Air;T=T[8];P=P[8])
ss9=s[8]
P[9] = P_r*P[8]
Ts9=temperature(Air;s=ss9;P=P[9])
Eta_comp = w_gas_comp_isen/w_gas_comp "Definição de eficiência adiabática do compressor"
h[8] + w_gas_comp_isen =hs9
h[8]=ENTHALPY(Air;T=T[8])
hs9=ENTHALPY(Air;T=Ts9)
h[8] + w_gas_comp = h[9]
T[9]=temperature(Air;h=h[9])
s[9]=ENTROPY(Air;T=T[9];P=P[9])
"Análise do trocador de calor no ciclo a gás"
h[9] + q_e = h[10]
h[10]=ENTHALPY(Air;T=T[10])
P[10]=P[9]
Q_dot_e=m_dot_gas*q_e
"Análise da turbina a gás"
s[10]=ENTROPY(Air;T=T[10];P=P[10])
ss11=s[10]
P[11] = P[10] /P_r
Ts11=temperature(Air;s=ss11;P=P[11])
Eta_gas_turb = w_gas_turb /w_gas_turb_isen "Definição de eficiencia isentrópica para a turbina a gás"
h[10] = w_gas_turb_isen + hs11
hs11=ENTHALPY(Air;T=Ts11)
h[10] = w_gas_turb + h[11]
T[11]=temperature(Air;h=h[11])
s[11]=ENTROPY(Air;T=T[11];P=P[11])
"Trocador de calor gás-vapor"
m_dot_gas*h[11] + m_dot_vapor*h[4] = m_dot_gas*h[12] + m_dot_vapor*h[5]
h[12]=ENTHALPY(Air; T=T[12])
s[12]=ENTROPY(Air;T=T[12];P=P[12])
"Análise do ciclo a vapor"
"Análise da bomba 1"
Fluid$='STEAM'
P[1] = P[7]
P[2]=P[6]
h[1]=enthalpy(Fluid$;P=P[1];x=0)
v1=volume(Fluid$;P=P[1];x=0)
s[1]=entropy(Fluid$;P=P[1];x=0)
T[1]=temperature(Fluid$;P=P[1];x=0)
w_bomba1_s=v1*(P[2]-P[1])
w_bomba1=w_bomba1_s/Eta_bomba "Definição de eficiência da bomba"
h[1]+w_bomba1= h[2]
s[2]=entropy(Fluid$;P=P[2];h=h[2])
T[2]=temperature(Fluid$;P=P[2];h=h[2])
"Anális do reaquecedor de água"
y*h[6] + (1-y)*h[2] = 1*h[3]
P[3]=P[6]
h[3]=enthalpy(Fluid$;P=P[3];x=0)
T[3]=temperature(Fluid$;P=P[3];x=0)
s[3]=entropy(Fluid$;P=P[3];x=0)
"Análise da bomba 2"
P[4] = P[5]
v3=volume(Fluid$;P=P[3];x=0)
w_bomba2_s=v3*(P[4]-P[3])
w_bomba2=w_bomba2_s/Eta_bomba
h[3]+w_bomba2= h[4] "Steady-flow conservation of energy"
s[4]=entropy(Fluid$;P=P[4];h=h[4])
T[4]=temperature(Fluid$;P=P[4];h=h[4])
w_vapor_bombas = (1-y)*w_bomba1+ w_bomba2
"Análise da turbina a vapor"
h[5]=enthalpy(Fluid$;T=T[5];P=P[5])
s[5]=entropy(Fluid$;P=P[5];T=T[5])
ss6=s[5]
hs6=enthalpy(Fluid$;s=ss6;P=P[6])
Ts6=temperature(Fluid$;s=ss6;P=P[6])
h[6]=h[5]-Eta_vapor_turb*(h[5]-hs6)
T[6]=temperature(Fluid$;P=P[6];h=h[6])
s[6]=entropy(Fluid$;P=P[6];h=h[6])
ss7=s[5]
hs7=enthalpy(Fluid$;s=ss7;P=P[7])
Ts7=temperature(Fluid$;s=ss7;P=P[7])
h[7]=h[5]-Eta_vapor_turb*(h[5]-hs7)
T[7]=temperature(Fluid$;P=P[7];h=h[7])
s[7]=entropy(Fluid$;P=P[7];h=h[7])
h[5] = w_vapor_turb + y*h[6] +(1-y)*h[7]
"Análise do condensador"
(1-y)*h[7]=q_s+(1-y)*h[1]
Q_dot_s=m_dot_vapor*q_s
"Análise do ciclo"
RelacaoMassica_gasparavapor =m_dot_gas/m_dot_vapor
W_dot_liq=m_dot_gas*(w_gas_turb-w_gas_comp)+ m_dot_vapor*(w_vapor_turb -w_vapor_bombas)
Eta_th=W_dot_liq/Q_dot_e
Bwr=(m_dot_gas*w_gas_comp + m_dot_vapor*w_vapor_bombas)/(m_dot_gas*w_gas_turb + m_dot_vapor*w_vapor_turb)
W_dot_liq_vapor = m_dot_vapor*(w_vapor_turb - w_vapor_bombas)
W_dot_liq_gas = m_dot_gas*(w_gas_turb - w_gas_comp)
RazaoTrabalhoLiq_gasparavapor = W_dot_liq_gas/W_dot_liq_vapor
Passo 3
Então, com o código do passo 2, conseguir obter uma relação entre a razão de pressão e os fluxos de massa de ar e vapor sobre a eficiência térmica do ciclo. Esse comportamento está ilustrado na tabela paramétrica a seguir:
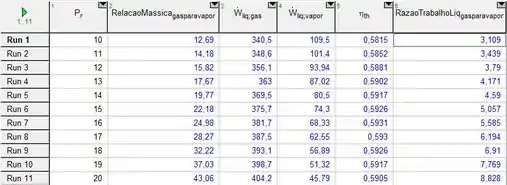
E, o gráfico que relaciona a razão de pressão e o fluxo de massa de ar e vapor é:
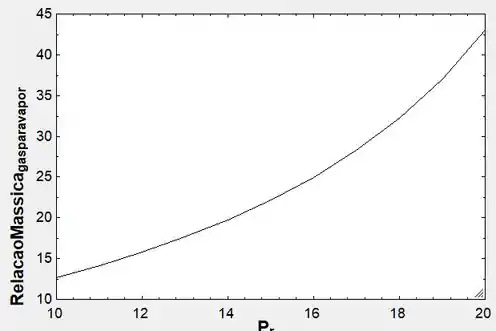
Resposta
Ei, a resposta está no passo a passo :)