Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 10.Problemas - Ex. 103
Repita o Prob. 10-102, considerando uma eficiência isentrópica de 85% para as turbinas e de 100% para as bombas.
Passo 1
Tá legal, vamos primeiro ilustras o ciclo descrito no enunciado juntamente com seu diagrama T-s, então, teremos:
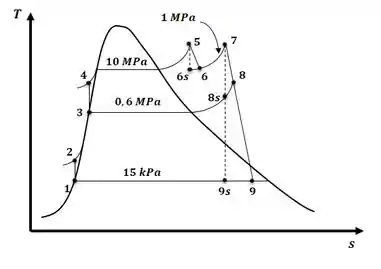
Agora, o que nós vamos fazer é encontrar o valor das propriedades de interesse com as temperaturas e pressões fornecidas no enunciado com a ajuda das tabelas do apêndice A, então, teremos:
Com isso, podemos encontrar o trabalho produzido pela bomba 1 através de:
E, com esse valor, aplicando o equilíbrio de energia para a bomba 1, podemos encontrar o valor da entalpia no ponto 2:
Agora, continuando com as propriedades, temos:
Com isso, podemos encontrar o trabalho produzido pela bomba 2 através de:
E, com esse valor, aplicando o equilíbrio de energia para a bomba 2, podemos encontrar o valor da entalpia no ponto 4:
Agora, continuando com os pontos de interesse, temos:
Então, considerando primeiramento a expansão 5-6 na turbina como isentrópica, temos:
E, agora, sabemos que a eficiência isentrópica da turbina pode ser escrita como:
E, isolando a entalpia real no ponto 6, temos:
Substituindo os valores conhecidos, temos:
Passo 2
Agora, continuando com as propriedades, temos:
Então, novamente, da eficiência isentrópica da turbina para o processo 7-8, temos:
E, isolando a entalpia real no ponto 8, temos:
Substituindo os valores conhecidos, temos:
E, da mesma forma, para o ponto 9, temos:
Agora, supondo o processo 7-9 isentrópico, podemos encontrar seu título nessa situação através de:
E, com esse valor de título, podemos encontrar a entalpia para o ponto 9:
Então, pela relação isentrópica da turbina para o processo 7-9, temos:
E, isolando a entalpia real no ponto 9, temos:
Substituindo os valores conhecidos, temos:
Agora, com todas as propriedades determinadas, podemos aplicar o equilíbrio de energia para o aquecedor de água, então, teremos:
Como no nosso caso temos regime permanente, então , dessa forma, a equação se torna:
E, colocando em função das entalpias e das vazões mássicas, temos:
Escrevendo a equação anterior em função da fração mássica extraída para o aquecedor, temos:
Substituindo os valores conhecidos, temos:
Passo 3
Agora, podemos calcular o calor que entra no sistema pela caldeira e devido ao reaquecimento, então, escrevendo em função da diferença de entalpia nesses pontos, temos:
E o calor que sai do sistema através do condensador será:
E, a eficiência térmica pode ser encontrada através de: