Enunciado
Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 11.Problemas - Ex. 54
Repita o Problema 11.53, mas considere calor específico variável. As tabelas de gás ideal, Tabela A.7, são recomendadas para esse cálculo (e o calor específico da Fig. 5.10 para altas temperaturas).
Passo 1
Fala, galera! Vamos resolver essa questão.
Vamos começar dando uma olhada no diagrama do processo:
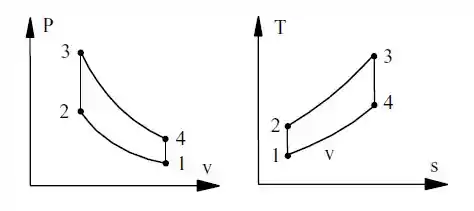
Agora nós vamos considerar o calor específico variável, então vamos dar uma olhadinha na Tabela A.7 para pegar as propriedades:
No processo de compressão isentrópica (), de 1 para 2, temos:
Desse modo,
Devemos agora, chutar um e obter na Tabela A.7 para essa temperatura, e por tentativa e erro devemos igualar os dois lados da equação:
Vamos chutar:
Na equação:
Assim, obtemos
Passo 2
Seguindo calcularemos o trabalho de compressão:
Pela transferência de calor, podemos calcular :
Pela Tabela A.7, para essa energia interna, obtemos a temperatura máxima possível:
Com os dados obtidos, conseguimos calcular a pressão máxima também:
Passo 3
Agora vamos analisar a expansão isentrópica:
Pelo mesmo método de tentativa e erro, vamos descobrir :
Sabendo que:
Temos:
Desse modo,
Devemos agora, chutar um e obter um na Tabela A.7 para essa temperatura, e por tentativa e erro devemos igualar os dois lados da equação:
Chute:
Na equação:
Que é igual ao que calculamos. Assim, obtemos:
Agora, calcularemos o trabalho de expansão:
Passo 4
Por fim, o problema nos pede o rendimento térmico e a pressão média efetiva do ciclo.
Vamos primeiro determinar o rendimento:
Para calcular a pressão média efetiva, vamos precisar determinar o deslocamento volumétrico nos estados 1 e 2. No estado 1, temos:
Usando a relação de compressão, temos:
E a pressão média efetiva será:
E concluímos o exercício. Valeu, galera! 😉