Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 11.Problemas - Ex. 82

Repita o Problema 11.81, porém considerando que o hélio é o fluido de trabalho do ciclo em vez do ar. Discuta o significado dos resultados.

Passo 1

Fala, galera! Vamos resolver essa questão.

Vamos começar analisando dois diagramas que representam, respectivamente, o processo que ocorre na máquina e o ciclo de refrigeração:

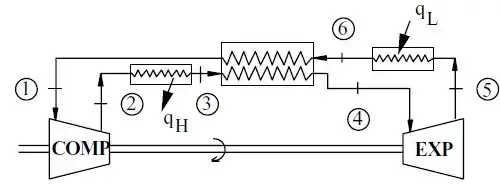
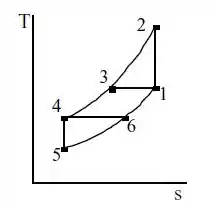
Por meio dos diagramas é possível obter T 1 = T 3 = 15   ° C = 282,2   K e:

P 1 = 100   k P a

P 2 = 1,4   M P a

T 4 = T 6 = - 50   ° C = 223,2   K

Estabelecidos os dados, agora vamos às equações!

Passo 2

Primeiramente, note que o compressor, isentrópico s 2 = s 1 , nos dá a temperatura por meio da relação:

T 2 = T 1 P 2 P 1 k - 1 k

T 2 = 288,2   1400 100 0 , 40

T 2 = 828,2   K

Logo, para o compressor vamos ter o trabalho específico:

w c = - w 1 → 2 = C p 0 T 2 - T 1

w c = 5,193 ∙ 828,2 - 288,2

w c = 2804,1   k J / k g

Passo 3

Na turbina, também temos uma expansão isentrópica, com s 5 = s 4 , que nos fornece:

T 5 = T 4 P 5 P 4 k - 1 k

T 5 = 223,2 100 1400 0 , 40

T 5 = 77,7   K

Assim, para o trabalho específico, temos:

w E = C p 0 T 4 - T 5

w E = 5,193 ∙ 223,2 - 77,7

w E = 755,5   k J / k g

Com esses dois dados, podemos obter o trabalho líquido do ciclo, fazendo:

w l í q = w E - w c

w l í q = 7 55,5 - 2804,1

w l í q = - 2048,6   k J / k g

Passo 4

Agora vamos calcular a taxa de transferência de calor q L :

q L = C p 0 T 6 - T 5

q L = w E

q L = 755,5   k J / k g

Dessa forma, podemos determinar o coeficiente de desempenho do ciclo:

β = q L w l í q

β = 755,5 2048,6

β = 0 , 369

Observe que a baixa temperatura é mais baixa que no problema anterior e os termos de trabalho mais altos do que com o ar. Isso se deve à capacidade térmica C p 0 e à relação de aquecimento específico ( k = 1   2 / 3 ). O custo é um C O P mais baixo que requer mais trabalho por k J de resfriamento.

Prontinho! Até a próxima, galera!

Resposta

β = 0,369

Exercícios de Livros Relacionados

51 Um inventor afirma ter desenvolvido uma unidade de refrigeração que mantém o espaço refrigerado a -10°C enquanto opera numa sala onde a temperatura é 25°C e apresentando, nestas condições, um coefi
63 Um escoamento de água, com vazão em massa igual a 60 kg/h, deve ser vaporizado a pressão constante. A transferência de calor para a água é fornecida por uma bomba de calor. Essa bomba utiliza um re
57 O hélio apresenta o mais baixo ponto de ebulição normal entre todos os elementos (4,2 K). O hélio, nesta temperatura, apresenta entalpia de vaporização igual a 83,3 kJ/kmol. Um ciclo de refrigeraçã
55 A temperatura mais baixa obtida até hoje é da ordem de 1 × 10 - 6 K . Para atingir essa temperatura, um estágio adicional é inserido no processo descrito no Prob. 7.54. Este estágio é conhecido por
53 É necessário, numa experiência criogênica, manter a temperatura de um recipiente a -125 °C enquanto o meio, a 20°C, transfere 100 W de calor ao recipiente. Qual a mínima potência necessária para ac