Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Van Wylen- Ed: 6º - Capítulo 2.Problemas - Ex. 84

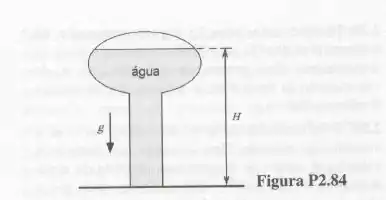
O reservatório d’água de uma cidade é pressurizado com ar a 125   k P a e está mostrado na Fig. P2.84 A superfície livre do líquido está situada a 35   m do nível do solo. Admitindo que a massa específica da água é igual a 1000   k g / m 3 e que o valor da aceleração da gravidade é o normal, calcule a pressão mínima necessária para o abastecimento do reservatório.

Passo 1

Temos a pressão do ar P a r = 125   k P a a pressão da coluna de água.

Vamos calcular a pressão da coluna de água e somar com a pressão do ar e está será pressão mínima que terá de ser fornecida para abastecer o reservatório.

Passo 2

Aplicando Bernoulli na coluna de água, temos:

Δ P = ρ g H

Substituindo o g = 9,8   m / s 2 , H = 35   m e ρ = 1000   k g / m 3 , fica:

Δ P = 1000 ∙ 9,8 ∙ 35

Δ P = 343   k P a

Passo 3

Somando pressão do ar com a pressão da coluna de água, temos:

Δ P n e c e s s á r i o = 343   k P a + 125 k P a = 468   k P a  

Resposta

Δ P n e c e s s á r i o = 468   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Expresse a lei de Pascal e de um exemplo pratico para ela.
Determine a pressao atmosferica em um local onde a leitura barometrica e de 750   m m   H g . Considere a densidade do mercúrio como 13.600 k g / m 3 .
A pressão de vácuo de um condensador e 80k P a . Se a pressão atmosférica e 98k P a , qual e a pressão manométrica e a pressão absoluta em k P a ,k N / m 2 , l b f / p e 2 , p s i , em mH g ?
Alguém diz que a pressão absoluta de um liquida de densidade constante dobra quando a profundidade dobra. Você concorda com essa afirmação? Explique.
Um medidor de vácuo conectado a um tanque indica 30   k P a em uma localização na qual a leitura barométrica e de 750   m m   H g . Determine a pressão absoluta no tanque. Considere ρ H g = 13 590   k