Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 8.Problemas - Ex. 131
Um tanque de volume constante está a , e um dispositivo mantido a uma pressão constante está a . Tanto o tanque como o dispositivo contem de ar. Uma máquina térmica colocada entre o tanque e o dispositivo recebe calor do tanque de maior temperatura, produz trabalho e rejeita calor para o tanque com menor temperatura. Determine o trabalho máximo que pode ser produzido pela máquina térmica e as temperaturas finais do tanque e do dispositivo. Considere calores específicos constantes a temperatura ambiente.
Passo 1
Vamos lá! A questão nos afirma que um motor térmico funciona entre um tanque e um cilindro cheio de ar a diferentes temperaturas. O trabalho máximo que pode ser produzido e as temperaturas finais devem ser determinadas.
Podemos representar o problema como
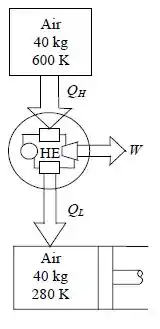
Assumindo que:
- O ar é um gás ideal com aquecimento específico constante à temperatura ambiente.
Os aquecedores de ar específicos (Tabela A-2).
Passo 2
Pronto já temos todas as informações necessárias, vamos para a análise. Desse modo temos que para a produção máxima de energia, a geração de entropia deve ser zero. Tomamos como sistema o tanque, o cilindro (a fonte de calor e o dissipador de calor) e o motor térmico. Observando que o sistema não envolve transferência de calor e massa e que a mudança de entropia para dispositivos cíclicos é zero, o balanço da entropia pode ser expresso como
Então
onde e são as temperaturas iniciais da fonte e do lavatório, respectivamente, e é a temperatura final comum. Portanto, a temperatura final dos tanques para a produção máxima de energia é
Passo 3
Portanto para a fonte:
E para o lavatório:
Então o trabalho produzido torna-se
Portanto, um máximo de de trabalho pode ser produzido durante este processo.