Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 10.Problemas - Ex. 98
Uma usina de potência a vapor opera segundo um ciclo de Rankine ideal com dois estágios de reaquecimento e produz uma potência líquida de 75 MW. Vapor entra em todos os três estágios da turbina a 550 °C. A pressão máxima do ciclo é de 10 MPa, e a pressão mínima é de 30 kPa. O vapor é reaquecido a 4 MPa na primeira vez, e a 2 MPa na segunda. Mostre o ciclo em um diagrama T-s que inclua as linhas de saturação e determine (a) a eficiência térmica do ciclo e (b) o fluxo de massa do vapor.
Passo 1
Tá legal, vamos primeiro ilustrar o diagrama T-s do ciclo Rankine com dois estágios de reaquecimento:
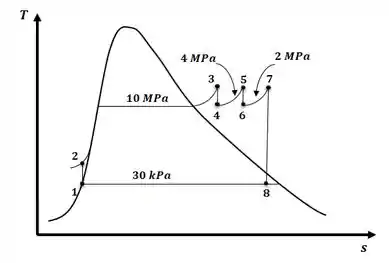
Agora, o que nós vamos fazer é encontrar o valor das propriedades de interesse com as temperaturas e pressões fornecidas no enunciado com a ajuda das tabelas do apêndice A, então, teremos:
Com isso, podemos encontrar o trabalho produzido pela bomba através de:
E, com esse valor, aplicando o equilíbrio de energia para a bomba, podemos encontrar o valor da entalpia no ponto 2:
Agora, continuando com as propriedades, temos:
Então, com esses dados do ponto 8, podemos encontrar o título nesse ponto através de:
E, com esse título, podemos encontrar a entalpia nesse ponto:
Passo 2
Agora, com os valores das propriedades, vamos encontrar o calor que entra e o que sai do sistema através da diferença entre as entalpias nesses pontos, lembrando que, como temos 2 estágios, teremos 3 pontos onde o calor entra no sistema, então teremos:
E, o calor que sai será:
E, agora, podemos encontrar o trabalho líquido produzido pelo sistema, que será a diferença entre o calor que entra e que sai do sistema, então, temos:
E, com esse valor, podemos encontrar a eficiência do sistema, que será:
Passo 3
Agora, para encontrar a vazão mássica de vapor no sistema, vamos utilizar o a potência líquida fornecida no enunciado e o trabalho específico líquido encontrado no passo 2, então, teremos: