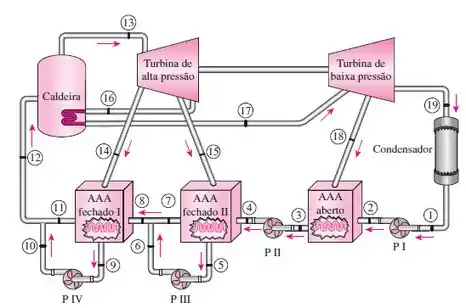
Uma usina de potência a vapor operando segundo um ciclo de Rankine ideal com reaquecimento e regeneração com três aquecedores de água de alimentação, como mostrado na figura, mantém a caldeira a 6000 kPa, o condensador a 7,5 kPa, o reaquecedor a 800 kPa, o aquecedor de água de alimentação fechado mantido a alta pressão a 3000 kPa, o aquecedor de água de alimentação fechado mantido a baixa pressão a 1800 kPa e o aquecedor de água de alimentação aberto mantido a 100 kPa. A temperatura à entrada de ambas as turbinas é de 500 °C. Determine as seguintes grandezas para esse sistema por unidade de fluxo de massa através da caldeira.
(a) O fluxo de massa necessário para manter a alta pressão, o aquecedor de água de alimentação fechado.
(b) O fluxo de massa necessário para manter a baixa pressão, o aquecedor de água de alimentação fechado.
(c) O fluxo de massa necessário para manter o aquecedor de água de alimentação aberto.
(d) O fluxo através do condensador.
(e) O trabalho produzido pela turbina de alta pressão.
(f) O trabalho produzido pela turbina de baixa pressão.
(g) O calor fornecido na caldeira e no reaquecedor.
(h) O calor rejeitado no condensador.
(i) A eficiência térmica.
Passo 1
Tá legal, o que precisamos fazer primeiro é encontrar as propriedades nos pontos de interesse com as pressões e temperaturas dadas no enunciado com a ajuda das tabelas do apêndice A, então, vamos lá:
Com isso, podemos encontrar o trabalho consumido pela bomba 1 através de:
E, com esse valor, aplicando o equilíbrio de energia para a bomba 1, podemos encontrar o valor da entalpia no ponto 2:
Agora, continuando com as propriedades, temos:
Com isso, podemos encontrar o trabalho consumido pela bomba 2 através de:
E, com esse valor, aplicando o equilíbrio de energia para a bomba 2, podemos encontrar o valor da entalpia no ponto 4:
Agora, continuando com os pontos de interesse, temos:
Com isso, podemos encontrar o trabalho consumido pela bomba 3 através de:
E, com esse valor, aplicando o equilíbrio de energia para a bomba 3, podemos encontrar o valor da entalpia no ponto 6:
Agora, continuando com os pontos de interesse, temos:
Com isso, podemos encontrar o trabalho consumido pela bomba 4 através de:
E, com esse valor, aplicando o equilíbrio de energia para a bomba 4, podemos encontrar o valor da entalpia no ponto 10:
Passo 2
Agora, continuando com as propriedades, temos:
E, com esses valores para o ponto 19, podemos encontrar seu título através de:
E, com esse valor de título, podemos encontrar a entalpia no ponto 19:
Agora, analisando os reaquecedores de água, sabemos que a água deve ser reaquecida até a temperatura de extração do vapor, o que faz com que fiquem como líquido saturado na saída. Dessa forma, teremos:
Passo 3
Agora, vamos aplicar as equações de equilíbrio de energia para os dispositivos do ciclo e formar um sistema de equações a ser resolvido no EES. Então, começando pelo balanço de massa na turbina de alta pressão, temos:
Em que é a fração mássica extraída para o aquecedor fechado 1, é a fração extraída para o aquecedor fechado 2 e é a fração que vai para o reaquecimento na caldeira e depois para a turbina de baixa pressão. Agora, para a turbina de baixa pressão, temos:
Em que é a fração mássica que vai para o aquecedor aberto e é a fração mássica que vai para o condensador. Agora, aplicando um equilíbrio de energia para o aquecedor aberto, temos:
Aplicando o equilíbrio de energia para o aquecedor fechado 2, temos:
Aplicando o equilíbrio de energia para o aquecedor fechado 1, temos:
Aplicando o equilíbrio de energia para a saída do aquecedor fechado 2, temos:
E, por fim, aplicando o equilíbrio de energia para a saída do aquecedor fechado 1, temos:
Então, usando um programa computacional para resolver esse sistema de equações encontrado simultaneamente, chegamos em:
Então, para a letra (a), que pede o fluxo de massa necessário para manter a alta pressão, o aquecedor de água de alimentação fechado, teremos que o fluxo de massa será:
Passo 4
Agora, para a letra (b) o fluxo de massa necessário para manter a baixa pressão, o aquecedor de água de alimentação fechado será:
Passo 5
Para a letra (c), o fluxo de massa necessário para manter o aquecedor de água de alimentação aberto será:
Passo 6
E, o fluxo através do condensador pedido na letra (d) será:
Passo 7
Agora, para calcular o trabalho produzido pela turbina de alta pressão, vamos utilizar as entalpias conhecidas e as frações mássicas obtidas no passo 3, então, teremos:
Substituindo os valores conhecidos, temos:
Passo 8
Agora, para calcular o trabalho produzido pela turbina de baixa pressão, vamos utilizar as entalpias conhecidas e as frações mássicas obtidas no passo 3, então, teremos:
Substituindo os valores conhecidos, temos:
Passo 9
Agora, o calor que entra no sistema é dado pelo equilíbrio de energia na caldeira, entre os pontos 12 e 13 e depois com o reaquecedor entre os pontos 16 e 17, então, temos:
Substituindo os valores conhecidos, temos:
Passo 10
O calor que sai do sistema pode ser encontrado aplicando-se o equilíbrio de energia para o condensador, então, teremos:
Passo 11
E, finalmente, podemos encontrar a eficiência do sistema através de: