Reconsidere o Prob. 10-66. Usando o EES (ou outro programa), resolva esse problema com o recurso de entrada de dados na janela do diagrama do EES. Inclua os efeitos das eficiências da turbina e da bomba para avaliar as irreversibilidades associadas a cada um dos processos. Mostre o ciclo em um diagrama T-s que inclua as linhas de saturação. Discuta os resultados de seus estudos paramétricos.
Passo 1
Tá legal! A primeira coisa que vamos fazer é ilustrar o ciclo Rankine ideal com reaquecimento e o seu diagrama T-s com a figura a seguir fornecida nessa seção do livro:
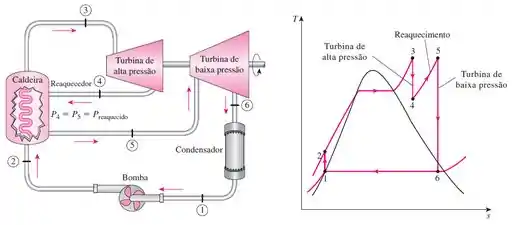
Agora, com os valores dos pontos fornecidos, vamos usar esses valores conhecidos no código do EES para obter as propriedades e, em seguida, programar a análise feita no Prob. 10-66, só que no próprio EES, o passo a passo é o mesmo, só que agora o programa vai fazer o trabalho de procurar o valor das propriedades e de efeturar os cálculos para nós.
Passo 2
Sendo assim, o código no EES que resolve o nosso problema será:
"Dados fornecidos no problema"
P[6] = 20 [kPa]
P[3] = 6000 [kPa]
T[3] = 400 [C]
P[4] = 2000 [kPa]
T[5] = 400 [C]
Eta_t = 100/100 "Eficiência isentrópica da turbina"
Eta_b = 100/100 "Eficiência isentrópica da bomba"
"Dados fornecidos pelo problema"
T_o = 295 [K]
T_R_L = 295 [K]
T_R_H = 1500 [K]
"Análise da bomba"
Fluid$='STEAM' "Função que representa fluido de estudo"
P[1] = P[6]
P[2]=P[3]
x[1]=0
h[1]=enthalpy(Fluid$;P=P[1];x=x[1])
v[1]=volume(Fluid$;P=P[1];x=x[1])
s[1]=entropy(Fluid$;P=P[1];x=x[1])
T[1]=temperature(Fluid$;P=P[1];x=x[1])
W_b_s=v[1]*(P[2]-P[1])
W_b=W_b_s/Eta_b
h[2]=h[1]+W_b
v[2]=volume(Fluid$;P=P[2];h=h[2])
s[2]=entropy(Fluid$;P=P[2];h=h[2])
T[2]=temperature(Fluid$;P=P[2];h=h[2])
"Análise da turbina de alta pressão"
h[3]=enthalpy(Fluid$;T=T[3];P=P[3])
s[3]=entropy(Fluid$;T=T[3];P=P[3])
v[3]=volume(Fluid$;T=T[3];P=P[3])
s_s[4]=s[3]
hs[4]=enthalpy(Fluid$;s=s_s[4];P=P[4])
Ts[4]=temperature(Fluid$;s=s_s[4];P=P[4])
Eta_t=(h[3]-h[4])/(h[3]-hs[4])"Eficiência isentrópica da turbina"
T[4]=temperature(Fluid$;P=P[4];h=h[4])
s[4]=entropy(Fluid$;T=T[4];P=P[4])
v[4]=volume(Fluid$;s=s[4];P=P[4])
h[3] =W_t_hp+h[4]
"Análise da turbina de baixa pressão"
P[5]=P[4]
s[5]=entropy(Fluid$;T=T[5];P=P[5])
h[5]=enthalpy(Fluid$;T=T[5];P=P[5])
s_s[6]=s[5]
hs[6]=enthalpy(Fluid$;s=s_s[6];P=P[6])
Ts[6]=temperature(Fluid$;s=s_s[6];P=P[6])
vs[6]=volume(Fluid$;s=s_s[6];P=P[6])
Eta_t=(h[5]-h[6])/(h[5]-hs[6])
h[5]=W_t_lp+h[6]
x[6]=QUALITY(Fluid$;h=h[6];P=P[6])
"Análise da caldeira"
Q_e + h[2]+h[4]=h[3]+h[5]
"Análise do condensador"
h[6]=Q_s+h[1]
T[6]=temperature(Fluid$;h=h[6];P=P[6])
s[6]=entropy(Fluid$;h=h[6];P=P[6])
"Análise do ciclo"
W_liq=W_t_hp+W_t_lp-W_b
Eff=W_liq/Q_e
"Destruições de exergia por processo"
q_R_23 = - (h[3] - h[2]) "Processo 2-3"
i_23 = T_o*(s[3] -s[2] + q_R_23/T_R_H)
q_R_45 = - (h[5] - h[4]) "Processo 4-5"
i_45 = T_o*(s[5] -s[4] + q_R_45/T_R_H)
q_R_61 = (h[6] - h[1]) "Processo 6-1"
i_61 = T_o*(s[1] -s[6] + q_R_61/T_R_L)
i_34 = T_o*(s[4] -s[3])
i_56 = T_o*(s[6] -s[5])
i_12 = T_o*(s[2] -s[1])
Passo 3
Através desse código, conseguimos plotar o diagrama T-s pedido, no enunciado, então, teremos:

Podemos ver que ele possui a mesma natureza do diagrama T-s apresentado no livro e transcrito aqui lá no começo do passo 1.
Resposta
Ei, a resposta está no passo a passo :)