Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 6.Problemas - Ex. 21
Uma usina a vapor com uma potência líquida de 150 MW consome carvão a uma taxa de 60 tons/h. Considerando que o poder calorífico do carvão corresponde a 30.000 kJ/kg, determine a eficiência global dessa usina.
Passo 1
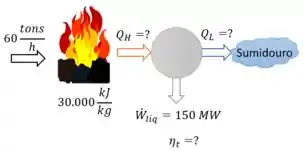
Primeiro, vamos calcular o calor gerado. Para isso vamos considerar que todo o carvão consumido é convertido em calor fornecido para a máquina. Então basta multiplicar a vazão mássica de carvão pelo seu poder calorífico:
Convertendo as toneladas em quilogramas e as horas em segundos:
Passo 2
A questão nos fornece o trabalho gerado pela turbina. Então vamos usar a equação 6-6 para determinar a eficiência:
Resposta
Exercícios de Livros Relacionados
a) Projete um amplificador inversor usando um amp op ideal cujo ganho é 4. Use um amp op ideal, um resistor de 30 kV no caminho de realimentação e fontes de alimentação de ;12 V. b) Utilizando o proje
Os dados seguintes são para uma usina termelétrica simples a vapor conforme mostrado na Fig. P 6.63 . O estado 6 tem x 6 = 0,92 e uma velocidade de 200m / s . A vazão de vapor é de 25k g / s , com 300
Um diagrama de fluxo simplificado para uma usina termelétrica nuclear é dada na Fig. P6.66. As vazões mássicas e os vários estados no ciclo são mostrados na seguinte tabela:O ciclo inclui alguns aquec
Um tanque rígido de 100l contém ar a 1M P a e 200° C . Uma válvula no tanque é então aberta e o ar escoa para fora até que a pressão caia para 100k P a . Durante este processo, calor é transferido de
Uma proposta é feita para a utilização de água quente geotérmica para operar uma turbina a vapor, conforme mostrado na Fig P6.70. A água de alta pressão a 1,5M P a e 180° C é estrangulada para dentro