Sistemas em equilíbrio
Teoria
Definição de equilíbrio
“Um sistema está em equilíbrio quando não existe a possibilidade dele efetuar trabalho quando isolado de seu meio.”
Essa definição é muito importante e a partir dela é possível achar uma propriedade interessante sobre o equilíbrio de sistemas. Para isso vamos ver como seria o cálculo do trabalho de um volume de controle qualquer onde a substância entra com uma dada vazão mássica , entalpia, temperatura e entropia.
A potência fornecida por este volume de controle será igual a
Onde maiúsculo é a velocidade de escoamento, a gravidade e a cota (altura).
Como a maioria dos sistemas que trabalhamos não possuem grandes diferenças de velocidade nem cota entre a entrada e a saída podemos cortar essas grandezas. Além disso, pela lei da continuidade (conservação da massa) vamos ter que a massa da entrada e da saída também será igual, com isso.
Pela definição de equilíbrio, tem-se que . Temos, também, que (função de Gibbs). Então nossa equação se reduz a:
Assim, no equilíbrio, e a temperatura e pressão constante teremos:
Olha só como a função de Gibbs é importante na definição de equilíbrio!
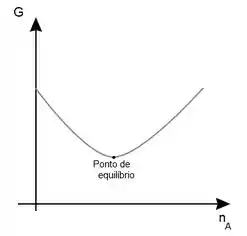
É legal ver como isso se mostra para uma reação química a pressão e temperatura constantes, onde a variação do número de mols de uma substância muda a energia de Gibbs. O equilíbrio acontecerá no ponto de derivada igual a zero, como mostrado no gráfico abaixo da função de Gibbs em função do número de mols de uma substância .
Substância pura
Quando estamos falando de uma substância pura então só faz sentido falar de equilíbrio entre suas fases. Utilizando a notação 1 e 2 para distinguir suas fases então vamos ter que.
Ou seja, a variação molar (em número de mols) da fase 1 é o oposto da variação molar da fase 2, o que faz sentido já que nessa análise estamos olhando apenas para o equilíbrio entre duas fases então se uma aumenta a outra diminui.
Como a variação da função de Gibbs é igual a variação molar () vezes a função de gibbs molar (), então vamos ter:
No equilíbrio vimos que , Logo:
Fazendo a substituição
Então
Isso significa que, no equilíbrio, as funções de Gibbs molares parciais de cada fase são iguais.
Também podemos definir o equilíbrio entre fases por meio da fugacidade, que, por ser independente da fase, ficaria da forma.
Solução ideal
Quando falamos de soluções ideais vamos ter que a fugacidade de um componente na mistura é igual à fração molar daquele componente vezes a fugacidade do componente puro no mesmo estado. Se compararmos os estados líquido e vapor vamos ter.
Analogamente para um outro componente
Onde representa a concentração da fase líquida e a concentração da fase vapor. Assim vamos ter também.
Regra de Raoult
A regra de Raoult é um modelo para soluções ideais a baixas pressões. Esse modelo se apoia em duas hipóteses simplificadoras, para o caso de um líquido, sendo elas:
- A primeira hipótese consiste na ideia de que fugacidade de um líquido A puro, a temperatura e pressão , é igual à fugacidade de A saturado (líquido ou vapor) a mesma temperatura e pressão de saturação correspondente . Podemos exprimir esta ideia da forma
- A segunda hipótese é de que o vapor saturado de A puro, a temperatura e pressão , se comporta como um gás perfeito.
Com isso vamos obter que, para um dado componente A, a fugacidade de A puro é igual a pressão de saturação
No caso de um vapor essa ideia se torna mais simples e podemos fazer diretamente a aproximação de que a fugacidade do vapor do componente A é igual a pressão
Como, no equilíbrio, temos
Então, para o caso de dois componentes, vamos ter
Juntamente com a equação que vimos anteriormente
Substância pura
Solução ideal
Regra de Raoult
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Água líquida e vapor d’água coexistem num recipiente na mesma temperatura e pressão. O que podemos afirmar sobre a energia de Gibbs de cada fase?
Passo 1
Como o sistema é composto por duas fases de uma substância pura em equilíbrio (pois estão a mesma temperatura e pressão), então a energia de Gibbs de ambas as fases é igual.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração própria
Um sistema é formado por dois reagentes que interagem numa reação química e formam um produto. Sabendo que a função de Gibbs varia de acordo com o número de mols desses componentes e que este sistema está a temperatura e pressão constantes, quando este sistema entrará em equilíbrio?
Passo 1
Como vimos na teoria um sistema está em equilíbrio quando .
O próprio enunciado afirma que a função de Gibbs varia de acordo com o número de mols desses componentes, portanto, deve existir um ponto onde a função de Gibbs é mínima e lembrando de cálculo 1 sua derivada é zero .
Logo, o sistema entrará em equilíbrio quando a a função de Gibbs for mínima.
Caso haja uma variação no número de mols de algum desses componentes o equilíbrio irá mudar consumindo mais reagentes ou consumindo o próprio produto (reação inversa).
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Elaboração própria
Um sistema formado por dois elementos e onde ambos coexistem em equilíbrio nos estados líquido e vapor. Sabendo que a pressão de saturação dos elementos e são, respectivamente, e que a concentação do líquido é igual a 0,3 e do vapor é 0,6. Calcule a pressão do sistema.
Passo 1
Nesse problema vamos utilizar a regra de Raoult porque ela expressão a pressão de saturação de um componente em função de sua concentração e da pressão total.
Como o problema deu , só falta achar a concentração do vapor . Para isso temos que
Logo
Passo 2
Agora é só substituir na equação
Resposta
Exercício Resolvido #4
Elaboração própria
Vimos que no equilíbrio não é possível a realização de trabalho e para o caso de um sistema sem variação de velocidade e altura teremos que . Mas agora imagine o caso em que existe uma variação expressiva de altura entre a entrada e a saída de um volume de controle, como ficará a equação do equilíbrio nesse caso?
Passo 1
O equilíbrio foi definido a partir do trabalho que pode ser realizado:
Com
Como neste caso há variação de altura porém não há variação da velocidade vamos ter que
E pela definição de equilíbrio
A massa se conserva logo,
Onde:
- é a variação da função de Gibbs.
- é a gravidade e a variação da altura entre a entrada e a saída.
Percebe que é impossível, neste caso, da função de Gibbs ser igual a zero.
Resposta
Exercício Resolvido #5
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.467 – Exercício 13.3. (adaptada)
Os estudos recentes indicam que a atmosfera de Titã, o maior satélite de saturno, é composta basicamente por nitrogênio e metano e que a pressão é igual a e as pressões de saturação do nitrogênio e metano são, respectivamente, 0,54 MPa e 0,02MPa. Admitindo que exista equilíbrio entre a atmosfera gasosa e o oceano líquido, determine quais são as composições da atmosfera e do oceano.
Passo 1
O problema pede a composição da atmosfera e do oceano ou seja, está pedindo a composição do oceano, fase líquida e portanto
e da atmosfera, fase vapor
Como a pressão de saturação e a pressão atmosférica também foram dadas então iremos utilizar a regra de Raoult
Passo 2
Agora vamos substituir na equação e ver o que achamos
Para o nitrogênio
Passo 3
Agora temos mais duas equações e com as duas equações das fases vapor e líquido temos 4 equações com 4 incógnitas:
Vamos substituir as duas últimas na primeira obtendo:
Multiplicando a segunda por 0,24 e subtraindo da primeira
Logo
Consequentemente para o metano
e para o nitrogênio
Resposta
Exercício Resolvido #6
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 15.21
Dióxido de carbono a 15 MPa é injetado no topo de um poço com 5 km de profundidade com conexão para um sistema de recuperação de petróleo. A coluna de flúido contido no poço possui temperatura constante de 40°C. Qual é a pressão na base do poço assumindo um comportamento de gás ideal? Dado: ;
Passo 1
Como visto no exercício anterior
Onde:
- é a variação da função de Gibbs.
- é a gravidade e a variação da altura entre a entrada e a saída.
Passo 2
A variação da energia potencial específica é dada por
Passo 3
A variação da função de Gibbs será
Como a entalpia pode ser escrita como então a variação da entalpia é zero, logo:
Lembrando que a variação da entropia para processos isotérmicos é
Então
Passo 4
Dessa forma podemos igualar os dois lados da equação
Resposta
Exercício Resolvido #7
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 15.22
Considere um poço de gás com profundidade de 2 km contendo uma mistura de metano e etano a temperatura uniforme de 30°C. A pressão no topo do poço é de 14 MPa e a composição na base molar é de 90% metano e 10% etano. Cada componente está no equilíbrio (de cima a baixo) com e assuma hipótese de gás ideal. Determine a pressão e a composição no fundo do poço. Dado: ; ; ;
Passo 1
Como o próprio problema já evidenciou temos que
Vamos aplicar essa equação tanto para o etano quanto para o metano, além disso vamos trabalhar com as grandezas levando em consideração o número de mols e a massa (diferentemente do exercício anterior no qual utilizamos as grandezas específicas). Assim vamos ter:
Para o metano
Para o etano
Passo 2
A variação da função de Gibbs será
Como a entalpia pode ser escrita como então a variação da entalpia é zero, logo:
Lembrando que a variação da entropia para processos isotérmicos é
Então
Passo 3
Utilizando a variação de Gibbs mostrada teremos:
E para o etano
Percebe aqui que temos de utilizar a pressão de cada componente. Mas aí, como estamos utilizando a hipótese de gases perfeitos, é só fazer
Para o etano
Passo 4
Agora basta substituir os valores e calcular a pressão e achar a composição, vamos fazer primeiro para o metano:
Repare que aqui utilizamos 2 ao invés de 2000 para trabalharmos com kJ como o resto das propriedades.
Para o etano
Passo 5
Portanto, a pressão total será igual a soma de
Passo 6
Para achar a composição faremos parecido com o final do passo 3.
Logo
Resposta
Exercício Resolvido #8
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 15.23
Um contâiner possui água líquida a 20°C e 100kPa em equilíbrio com uma mistura de ar seco e vapor d’água também a 20°C e 100kPa. De quanto é a pressão de vapor da água sabendo que a pressão de saturação da água nessas condições é de 2,339 kPa e o volume específico é 0,001002 m³/kg. Dados:
Passo 1
Sabemos que no equilíbrio a função de Gibbs é igual para as fases de vapor e líquida
Então o que vamos fazer é calcular a função de Gibbs da fase líquida e da fase vapor e igualar as duas.
Passo 2
Isso porque
Como o sistema não muda de volume nem temperatura temos
Voltando
Passo 3
Para o cálculo de vamos utilizar a mesma equação
Porém agora estamos falando de um gás e utilizando a hipótese de gás perfeito
Logo
Passo 4
Igualamos os dois termos