Projeção e Reflexão
Produzido por Bruno PestanaTeoria
Já vimos o que são autovalores e autovetores e como calcular eles. Aí você se pergunta:
Pô, tudo bem, eu ponho um vetor e sai um múltiplo dele, e aí? Pra que isso serve?
E aí que você pode entender o significado de uma matriz só olhando pros autovalores e autovetores dela! Olha essa matriz aqui, por exemplo:
Calculando os autovetores e autovalores dela chegamos ao vetor associado ao autovalor e ao autovetor associado ao autovalor (calcula aí!). Tá, mas o que isso quer dizer? Quer dizer que essa matriz é uma reflexão em torno do eixo !!
Mas da onde você tirou isso cara???

Veja bem, o que essa matriz faz é pegar as coordenadas de um vetor e multiplicar por enquanto mantém as coordenadas inalteradas!
Então, se aplicarmos ela ao vetor esperamos ter como retorno o vetor . Saca só:
E é isso o que acontece! Se ainda não conseguiu visualizar, olha as imagens aqui em baixo! A matriz é aplicada nos vetores azuis e leva nos vetores laranja.
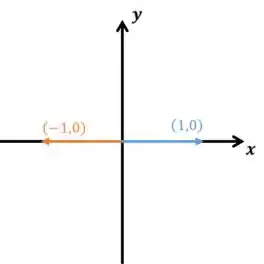
Agora olha essa:
Essa matriz possui o autovetor associado ao autovalor e o autovetor associado ao autovalor (calcula aí!). Então o que você acha que ela faz?
Se você disse que ela é uma projeção sobre a reta você está completamente correto!!
Essa matriz mantém inalterada a componente de um vetor que está sobre a reta e zera a componente sobre (ortogonal a ). Olha as imagens ai em baixo! Novamente, a matriz é aplicada no vetor azul e leva no laranja.
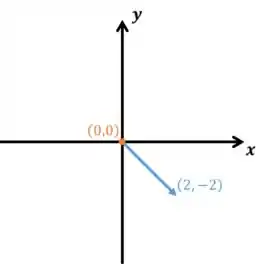
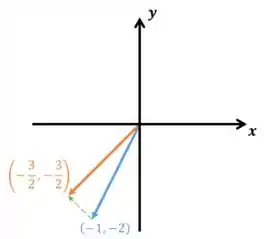

Demais né?! Agora se te perguntarem pra que uma matriz serve você já sabe como descobrir!
Autovetores e Autovalores da Projeção e da Reflexão
Acabamos de ver alguns exemplos de matrizes projeção e reflexão e vimos seus autovalores e autovetores. Agora vamos dar uma generalizada. Imagine uma base formada pela base de um conjunto com a base de (espaço perpendicular à ).
Se essa matriz representar a transformação de projeção, os vetores da base de serão autovetores associados ao autovalor ou . Já os vetores da base de serão autovetores associados ao autovalor ou .
Ou seja, quando um for o outro é e vice versa. Com o conhecimento que já temos, fica claro que isso não é coincidência. Se a projeção leva os vetores de um espaço no ela manterá os vetores do espaço ortogonal inalterados (autovalor )!!
O espaço associado ao autovalor será sempre o espaço aonde se está projetando!
Por outro lado, se essa matriz representar a transformação de reflexão, os vetores da base de serão autovetores associados ao autovalor ou . Já os vetores da base de serão autovetores associados ao autovalor ou .
Ou seja, quando um for o outro é e vice versa. Se pensarmos novamente no motivo disso veremos que se a reflexão leva os vetores de um espaço no inverso deles (autovalor ), ela manterá os vetores do espaço ortogonal inalterados (autovalor )!!
O espaço associado ao autovalor será sempre o espaço em torno do qual se está refletindo!
Podemos resumir isso na tabela abaixo:

Um macete interessante é que podemos saber a dimensão do espaço sobre o qual a matriz reflete ou projeta apenas pelo traço dela! Sabemos que o traço é a soma dos autovalores, e sabemos que a projeção tem apenas autovalores e , e a reflexão tem apenas autovalores e .
Imagine que você tem uma matriz de projeção com traço . Os autovalores tem que ser ! Logo, você está projetando num espaço de dimensão !
E se tivermos uma matriz reflexão com traço . Os autovalores tem que ser ! Então estaremos refletindo por uma reta!
Se você for curioso(a), você estará se perguntando agora quais são os autovalores de uma matriz rotação. Afinal as três principais transformações geométricas que vimos foram a projeção, a reflexão e a rotação, certo?
Bom, em geral as matrizes de rotação possuem autovalores complexos. No ela normalmente terá o autovalor (a reta em torno da qual estamos rodando) e um par de autovalores complexos (sim, autovalores complexos sempre vêm em pares). Já no em geral ela terá um par de autovalores complexos.
Obs.: Se a matriz possui apenas autovalores complexos isso significa que ela não preserva nenhuma direção e, portanto, não possui autovetores!
O único caso em que elas não terão autovalores complexos é quando forem uma rotação de ou de . Nesses casos elas assumirão o papel respectivamente de uma matriz reflexão e da matriz identidade ;)
Autovetores e Autovalores da Projeção e da Reflexão
Exercícios Resolvidos
Exercício Resolvido #1
Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 212 – Ext 7.2
Calcule os autovalores e autoespaços associados de:
uma reflexão no plano em ;
uma projeção ortogonal numa reta em com ;
uma projeção ortogonal na reta gerada por .
Passo 1
Bom, temos uma reflexão, então já sabemos que teremos autovalores e .
Ele já deu o plano em torno do qual estamos refletindo. Sabemos então que quaisquer dois vetores que formem uma base desse plano são autovetores associados ao autovalor .
Vamos achar uma base para esse plano então ;)
Logo, os vetores desse plano são da forma:
Então uma base para o plano será:
Logo, temos os autovetores e associados ao autovalor .
Passo 2
Já o autovalor está associado ao complemento ortogonal desse plano. Como estamos no , ele será a reta gerada pelo vetor que possui os coeficientes da equação do plano como coordenadas:
Então temos o autovetor associado ao autovalor .
Passo 3
Dessa vez temos uma projeção, então teremos os autovalores e .
Repare, no entanto, que ele não dá diretamente o espaço no qual estamos projetando. Opa, mas ele dá a informação que estamos projetando em uma reta e que:
Bom, disso tiramos que é autovetor associado ao autovalor . Isso quer dizer que esse vetor gera a reta na qual estamos projetando!!
Passo 4
Como estamos no , os vetores do plano ortogonal à essa reta serão autovetores associados ao autovalor . O plano ortogonal ao vetor tem equação dada pelas coordenadas do vetor:
Logo, esse plano possui vetores da forma:
Então temos os autovetores e associados ao autovalor .
Passo 5
Novamente temos uma projeção, então autovalores e . Ele já diz que a reta na qual estamos projetando é aquela gerada pelo vetor .
Temos então o autovetor associado ao autovalor .
Passo 6
Os autovetores associados ao autovalor serão aqueles do espaço ortogonal à reta. Como estamos no , esse espaço terá dimensão . E a melhor parte, aquele macete dos coeficientes também vale aqui! É só pegarmos as coordenadas do vetor e jogarmos nos coeficientes que teremos nosso espaço ortogonal:
Dessa forma temos os autovetores , e associados ao autovalor .
Resposta
Autovetor associado ao autovalor .
Autovetores e associados ao autovalor .
Autovetor associado ao autovalor .
Autovetores e associados ao autovalor .
Autovetor associado ao autovalor .
Autovetores , e associados ao autovalor .
Exercício Resolvido #2
UFRJ-P4-2012.2
Seja a projeção ortogonal sobre a direção do vetor seguida de uma expansão de na direção .
Os autovalores de são:
e
e
e
e
Passo 1
Bom, vamos por partes. Sabemos que o espaço gerado por é o eixo .
Isso quer dizer que a matriz projeta todos os vetores sobre o eixo . Logo, as coordenadas de todos os vetores serão zeradas. Conseguiu ver?
Bom, em seguida, temos uma expansão de na direção , ou seja, do eixo . Isso quer dizer que as coordenadas dos vetores serão dobradas. Só que como projetamos no eixo , não existem coordenadas ! Então essa expansão na realidade não faz absolutamente nada!!
Logo, é como se tivéssemos apenas a projeção, que como sabemos possui autovalores e . Então, a resposta é letra
Resposta
Exercício Resolvido #3
UFRJ-P4-2012.2
Seja a matriz que representa uma reflexão através do plano .
Marque a alternativa correta:
Os autovalores de são e
Os autovalores de são e
Os autovalores de são e
Os autovalores de são e
Passo 1
Mamatinha haha. Todas as matrizes reflexão possuem os autovalores e . E essa não seria diferente. Logo, letra .
Resposta
Letra .