Enunciado
Álgebra Linear e Geometria Analítica - Reginaldo - Matrizes, Vetores e Geometria Analítica- Ed: 1º - Capítulo 1.1 - Ex. 3b
(b) AEj é a j-esima coluna de A, para j = 1, 2, 3 e E B é a i-esima linha de B, para i = 1, 2, 3
Passo 1
Bem galera, essa questão é um pouco longa, então vamos aos poucos.
Basicamente vamos pegar a matriz A e multiplicar pela matriz E1, E2 e E3, uma de cada vez;
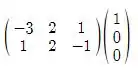
A*E1 =
Multiplicando vamos ter:
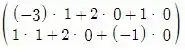
A*E1 =
Agora é só simplificar:
A*E1 =
Agora temos que fazer a mesma coisa para o A*E2 e para o A*E3.
Adiantando os passos:
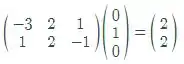
A*E2 =
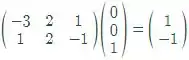
A*E3 =
Pronto, com essas matrizes vamos para o próximo passo.
Passo 2
Nessa etapa vamos precisar calcular as matrizes transpostas de E1, E2 e E3, vamo lá que vai ser bem fácil;
Transformamos uma matriz em transposta fazendo com que as linhas da matriz se torne as colunas e as colunas se torne as linhas;
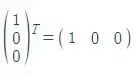
E1=
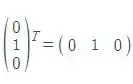
E2=
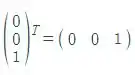
E3=
Passo 3
Agora vamos pegar as matrizes E1,E2,E3e multiplicar cada uma pela matriz B;
Vamos ter então:
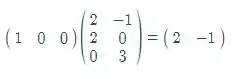
E1* B =
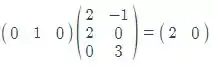
E2* B =
E3* B =
Passo 4
Agora para finalizar temos paro o A:
AE1 = -A[i=1] =
AE2 = -A[i=2] =
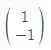
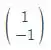
AE3 = -A[i=3] =
Temos para o B:
E1* B = [2 -1] -B[i=1] [2 -1] = 0
E2* B = [2 0] -B[i=2] [2 0] = 0
E3* B = [0 3] -B[i=3] [0 3] = 0
Finalizamos nossa questão aqui.Finalmente, vamos para a próxima ?
Resposta
Para o A temos:
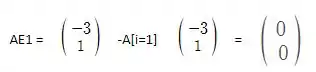
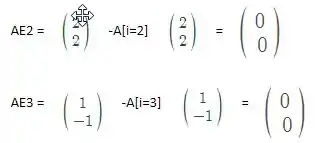
Para o B temos:
E1* B = [2 -1] -B[i=1] [2 -1] = 0
E2* B = [2 0] -B[i=2] [2 0] = 0
E3* B = [0 3] -B[i=3] [0 3] = 0