Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 4.10 - Ex. 14
Em cada parte, determine se o operador matricial definido pelas equações é injetor e, se for, encontre a matriz canônica do operador inverso e encontre .
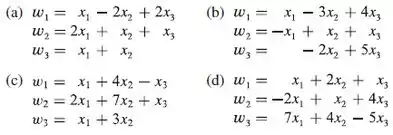
Passo 1
(a)
Vamos lá! vamos começar organizando nossa matriz canônica de , assim temos:
Como , pelo teorema nosso é injetora.
Agora vamos calcular nosso , assim temos.
Logo
Passo 2
(b)
Vamos lá! vamos começar organizando nossa matriz canônica de , assim temos:
Como a transformação não é injetora.
Passo 3
(c)
Vamos lá! vamos começar organizando nossa matriz canônica de , assim temos:
Como a transformação não é injetora.
Passo 4
(d)
Vamos lá! vamos começar organizando nossa matriz canônica de , assim temos:
Como , pelo teorema nosso não é injetora.
Isso é tudo pessoal! \o/
Até a próxima!
Resposta
(a)
(b) Não é injetora
(c) Não é injetora
(d) Não é injetora