Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 4.11 - Ex. 22
Em cada parte, encontre a matriz canônica do operador matricial
descrito pela figura.
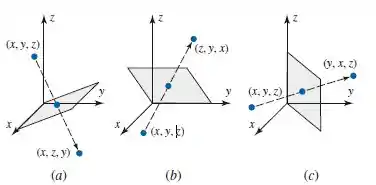
Passo 1
- Como se trata de uma reflexão sobre o plano , nossa matriz fica:
- Como se trata de uma reflexão sobre o plano , nossa matriz fica:
- Como se trata de uma reflexão sobre o plano , nossa matriz fica:
Passo 2
Passo 3
Resposta
Exercícios de Livros Relacionados
No exercício 7, verifique que P é uma matriz estocástica regular e encontre o vetor de estado estacionário da cadeia de Markov associada. P = 1 / 4 2 / 3 3 / 4 1 / 3
No exercício 5, em cada parte, determine se P é uma matriz estocástica regular. P = 1 / 5 1 / 7 4 / 5 6 / 7
No exercício 5, em cada parte, determine se P é uma matriz estocástica regular. P = 1 / 5 0 4 / 5 1
No exercício 8, verifique que P é uma matriz estocástica regular e encontre o vetor de estado estacionário da cadeia de Markov associada. P = 1 / 3 1 / 4 2 / 5 0 3 / 4 2 / 5 2 / 3 0 1 / 5
No exercício 3, use as Fórmulas (11) e (12) para calcular o vetor de estado x 4 de duas maneiras diferentes. P = 0,5 0,6 0,5 0,4 ;x 0 = 0,5 0,5