Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 7.3.Problemas Propostos - Ex. 2
Em cada um dos problemas 1 a 10, determinar o centro, os vértices, os focos e a excentricidade das hipérboles dadas. Esboçar o gráfico
Passo 1
Para questões de equações de hipérboles, vamos começar explicitando o que é o que.
- A equação está na forma onde são as coordenadas do centro.
- As coordenadas dos focos é dada pela equação
- Uma vez tendo o termo de e e as coordenadas do centro, temos os vértices e .
- A excentricidade é dada pela equação
- Para esboço do gráfico precisamos das assíntotas. Nesse caso é dada por
O eixo da hipérbole é o eixo que contém o sinal positivo na equação de forma
. Nesse caso, é o eixo .
Explicitando os fatores, vamos começar e encontra-los.
Passo 2
Analisando a equação , vemos que ela está no formato:
Portanto, daí conseguimos extrair as coordenadas do seu centro que são
Passo 3
Continuando na equação , por estar no formato , conseguimos também encontrar os fatores e .
Passo 4
Achando os fatores e , vamos jogar na equação para encontrarmos o fator .
Passo 5
Agora que achamos o fator , vamos usá-lo para encontrar a excentricidade da hipérbole.
Passo 6
Agora que todos os parâmetros foram encontrados, vamos encontrar os vértices e .
Assim,
Passo 7
Por fim, nos resta achar os focos antes de esboçar o gráfico. Assim, vamos usar as equações para os focos que explicitamos no Passo 1: e
Assim,
Passo 8
Com todos os pontos encontrados, vamos calcular as assíntotas usando a equação .
A segunda reta é dada por:
Passo 9
Por fim, vamos esboçar o gráfico. Para isso, usamos o Geogebra. Nesse caso, como os focos não são tão simples de serem marcados, vamos plotar o gráfico usando a equação da hipérole e as equações das assíntotas:
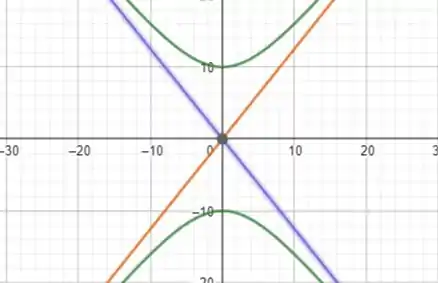
Pronto, é isso que a questão queria!
Resposta
e