Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 8.Elipse - Ex. 18
Em cada um dos problemas de 12 a 19, determinar uma equação da elipse que satisfaça as condições dadas. Esboçar o gráfico.
18. vértices e passando por ;
Passo 1
Vamos começar lembrando como é a fórmula da elipse:
Como ele diz que o vértices , temos , ou seja são os pontos no eixo y que valem -6 e 6, então podemos ver de cara que:
Passo 2
Show, sabendo disso, vamos reescrever nossa fórmula
Agora vamos pegar nosso ponto que pertence a elipse e substituir pelos pontos de :
Então nossa fórmula fica
Passando esse 8 para cima ficamos com
Passo 3
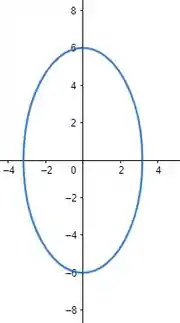
Esboçando isso ai ficamos com
Resposta
Exercícios de Livros Relacionados
Para as funções dadas f e g defina f / g e determine o domínio da função resultante. f x = x e g x = 1 x 2
Para as funções dadas f e g defina f / g e determine o domínio da função resultante. f x = 1 x - 3 e g x = x x + 1
Determine se a função é par, ímpar ou nem par e nem ímpar. f x = 2 x 3 - 3 x
Para as funções dadas f e g defina f + g e determine o domínio da função resultante. f x = 1 x - 3 e g x = x x + 1
Para as funções dadas f e g defina f ⋅ g e determine o domínio da função resultante. f x = x 2 - 9 e g x = x + 5