Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 8.Elipse - Ex. 19

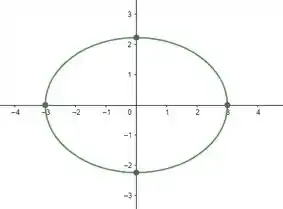
Em cada um dos problemas de 12 a 19, determinar uma equação da elipse que satisfaça as condições dadas. Esboçar o gráfico:

Centro C ( 0,0 ) , focos no eixo dos x , e = 2 3 e passando por P 2 , - 5 3

Passo 1

Vamos começar lembrando como é a fórmula da elipse:

x 2 a 2 + y 2 b 2 = 1

E vamos lembrar quem são nossos coeficientes

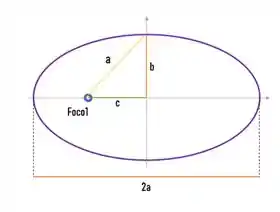
E ele diz que e (nossa excentricidade) é 2 3 e o e é ninguém mais ninguém menos que

e = c a

2 3 = c a

c = 2 a 3

E temos também, pelo triangulo a b c que

a 2 = b 2 + c 2

b 2 = a 2 - c 2

b 2 = a 2 - 2 a 3 2

b 2 = 5 a 2 9

Passo 2

Agora vamos colocar esse valor de b na formula da elipse e substituir x e y pelo ponto P

x 2 a 2 + y 2 5 a 2 9 = 1

x 2 a 2 + 9 y 2 5 a 2 = 1

Substituindo x e y , ficamos com:

2 2 a 2 + 9 - 5 3 2 5 a 2 = 1

4 a 2 + 9 * 25 9 5 a 2 = 1

4 a 2 + 5 a 2 = 1

a 2 = 9

Ufa! Agora que achamos a 2 , para descobrir b é só substituir em b 2 = 5 a 2 9

b 2 = 5 * 9 9

b 2 = 5

Então nossa equação fica:

x 2 9 + y 2 5 = 1

Podemos fazer o MMC e organizar essa equação para ficar

5 x 2 + 9 y 2 - 45 = 0

Passo 3

Esboçando isso dai ficamos com

Resposta

5 x 2 + 9 y 2 - 45 = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para as funções dadas f e g defina g / f e determine o domínio da função resultante. f x = 1 x - 3 e g x = x x + 1
Determine se a função é par, ímpar ou nem par e nem ímpar. F x = x 2 + 1 x 3 - x
Para as funções dadas f e g defina g ο f e determine o domínio da função resultante. f x = x 2 - 4 e g x = 4 x - 3
Para as funções dadas f e g defina f / g e determine o domínio da função resultante. f x = x 2 - 4 e g x = 4 x - 3
Para as funções dadas f e g defina f ⋅ g e determine o domínio da função resultante. f x = x e g x = 1 x 2