Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 7.1.Problemas Propostos - Ex. 9
Em cada um dos problemas 1 a 18, estabelecer a equação de cada uma das parábolas, sabendo que:
9. vértice: ; diretriz:
Passo 1
Como o vértice, , não está na origem e dessa vez não temos o foco, mas temos a diretriz, que é (uma reta “em pé”), então a parábola é deitada , então usamos a seguinte fórmula:
É praticamente igual à parabola com vértice na origem, mas:
Então ficamos com:
Passo 2
A gente já tem o vértice, ne... então:
E analisando a nossa parábola melhor vemos que ela tem a seguinte cara, onde F é o foco, V é o vértice e a linha vermelha é a diretriz:
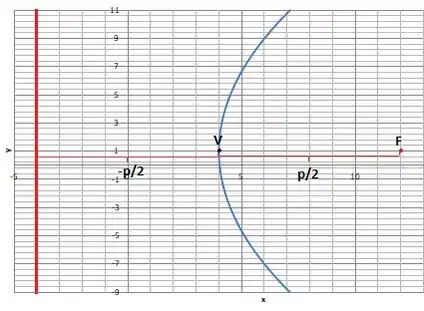
E pra achar o :
Então nossa equação fica:
Resposta
Exercícios de Livros Relacionados
Em cada um dos problemas 19 a 34, determinar o vértice, o foco, uma equação para a diretriz e uma equação para o eixo da parábola de equação dada. Esboçar o gráfico.23. y 2 = - 3 x
Em cada um dos problemas 1 a 18, estabelecer a equação de cada uma das parábolas, sabendo que:18. eixo paralelo a y = 0 e passa por P 1 - 2,4 ,P 2 - 3,2 e P 3 - 11 , - 2 .
Em cada um dos problemas 19 a 34, determinar o vértice, o foco, uma equação para a diretriz e uma equação para o eixo da parábola de equação dada. Esboçar o gráfico.26. y 2 + 4 y + 16 x - 44 = 0
Em cada um dos problemas 19 a 34, determinar o vértice, o foco, uma equação para a diretriz e uma equação para o eixo da parábola de equação dada. Esboçar o gráfico.27. y 2 + 2 y - 16 x - 31 = 0
Em cada um dos problemas 19 a 34, determinar o vértice, o foco, uma equação para a diretriz e uma equação para o eixo da parábola de equação dada. Esboçar o gráfico.19. x 2 = - 12 y