Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 8.Parábola - Ex. 32
Em cada um dos Problemas de 27 a 36, determinar a equação reduzida, o vértice, o foco, uma equação da diretriz e uma equação do eixo da parábola de equação dada. Esboçar o gráfico.
32.
Passo 1
A primeira coisa que precisamos fazer é reparar se é o ou o que está elevado ao quadrado. Como aqui é o que está elevado ao quadrado, então sabemos que o eixo é paralelo ao eixo . E a equação reduzida vai ter a cara:
Sendo:
Onde são as coordenadas do Vértice.
Passo 2
Vamos começar a resolver, então... Vamos deixar tudo que tem de um lado só e o resto do outro lado.
E, pra honra e glória da deusa, não precisamos completar o quadrado.
Podemos reescrever como:
Passo 3
- A equação reduzida, então vai ser:
E já conseguimos achar as coordenadas do vértice:
- O vértice fica:
Vamos já achar o ...
Passo 4
Vamos esboçar o gráfico, pois já temos o vértice e sabemos que o é positivo (então a parábola vai ter concavidade pra cima, uma carinha feliz). Isso vai facilitar muito achar as outras coisas, você vai ver...
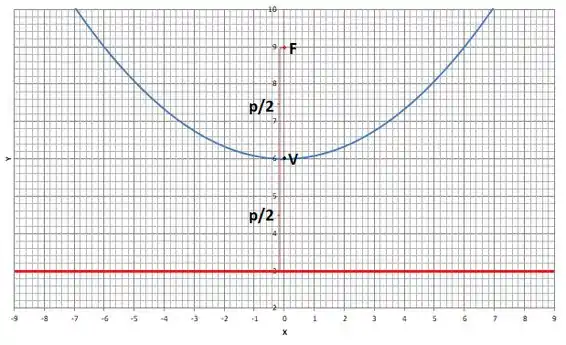
Reparei que como temos , então abaixo do vértice vai ser a diretriz (reta vermelha) e acima do vértice vai ser o foco (o foco fica sempre “dentro” da parábola, ne...). Então:
- O foco:
- A equação da diretriz:
- A equação do eixo da parábola (eixo de simetria, que divide a parábola em duas partes iguais):