Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 4.12 - Ex. 12d
Considere um processo de Markov com matriz de transição
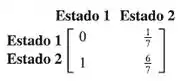
- Se o sistema tiver uma chanca de 50% de estar inicialmente no estado 1, com qual probabilidade ele estará no estado 2 na próxima observação?
Passo 1
Bom, para essa questão, as coisas se complicam um pouco, mas vamos começar pensando na probabilidade de estar inicialmente no estado 1 e, na próxima observação, ele estará no estado 2. Nesse caso, teremos a probabilidade de 100%.
Porém, há uma peculiaridade nessa questão, existe apenas uma chance de 50% de estar inicialmente no estado 1, com isso, sugere-se que façamos o seguinte,
Ou seja, há uma probabilidade de apenas 50% de ocorrer o evento.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Considere um processo de Markov com matriz de transiçãoO que representa a entrada 0,2?
Num dado dia, a qualidade do ar numa certa cidade é boa ou má. Os registros mostram que quando a qualidade do ar é boa num dado dia, então existe uma chance de 95% de que venha a ser boa no próximo di
Considere um processo de Markov com matriz de transiçãoSe inicialmente o sistema estiver no estado 1, com qual probabilidade ele estará no estado 2 na próxima observação?
Considere um processo de Markov com matriz de transiçãoSe o sistema tiver uma chance de 50% de estar inicialmente no estado 1, com qual probabilidade ele estará no estado 2 na próxima observação?
Um rato num experimento de laboratório pode escolher um entre dois tipos de comida a cada dia: o tipo I ou tipo II. Os registros mostram que se o rato escolhe o tipo I num certo dia, então a chance de