Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 2.Problemas - Ex. 7

Dado A = ( x , y ) com x ≠ y , observe que os pontos   B = x , x ,   C = ( y , x ) e D = ( y , y ) formam, juntamente com A, os vértices de um quadrado de lados paralelos aos eixos. A partir daí determine o simétrico de A relativamente à diagonal ∆   = x , x ; x   ∈ R .

Passo 1

Falaaaa, blz? Vamos fazer um desenho para nos ajudar a entender o que está ocorrendo.

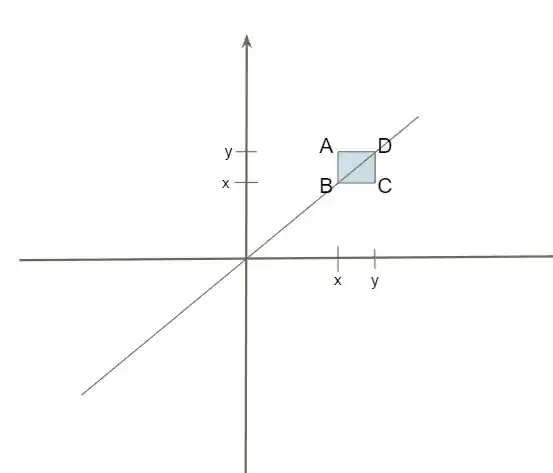
Passo 2

Veja que

∆   = x , x ; x   ∈ R

É a bissetriz dos quadrantes ímpares, como os lados são paralelos aos eixos, temos que diagonal pertence à bissetriz, ou seja, o simétrico de A em relação à bissetriz é simétrico à diagonal também.

Passo 3

Ou seja, queremos o ponto simétrico de A em relação à diagonal do quadrado

Pensando assim fica bem evidente que esse ponto é o próprio ponto C.

Além disso, veja que o ponto médio de A e C x + y 2 , x + y 2 ∈   ∆ ,     o u   s e j a ,   f a z   s e n t i d o   s e r   o   C

Resposta

C = ( y , x )

Exercícios de Livros Relacionados

Várias vezes, nas páginas anteriores, foi citada e usada a propriedade de que as diagonais de um paralelogramo cortam-se mutuamente ao meio. Dado um paralelogramo A B C D , escolha um sistema de coord
Considere o plano π : 2 x + 2 y - z = 0 .Determine as retas r, interseção do plano π com o plano yz, s, interseção do plano π com o plano xz e t, interseção do plano π com o plano z = 2. Desenhe um es