Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 2.Problemas - Ex. 9

Qual é o ponto da diagonal ∆ mais próximo de P = ( x , y ) ? E da diagonal ∆ ' ?

Passo 1

Primeiro vamos escrever que diagonais são essas:

∆   = x , x ; x   ∈ R

∆ ' = { x , - x ; x   ∈ R }

Passo 2

Quando pensamos em ponto mais próximos, pensamos em segmentos perpendiculares.

O ponto de uma reta, mais próximo do ponto P é aquele que quando ligado ao P forma um segmento perpendicular à reta, ilustrando numa imagem: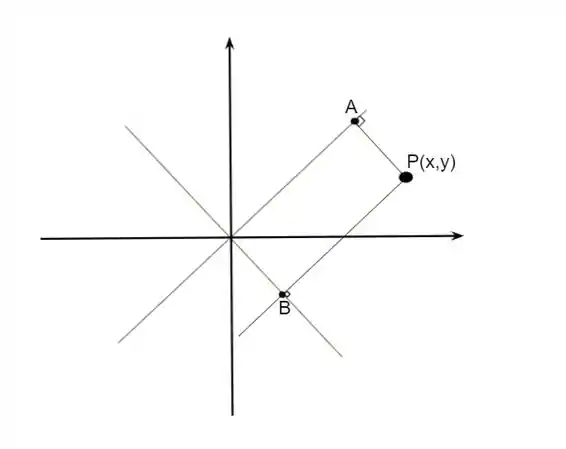

Onde A   ∈   ∆   e B ∈   ∆ '

Passo 3

Das outras 2 últimas questões nós achamos quem eram os simétricos de um ponto ( x , y ) em relação a cada uma dessas diagonais, obviamente que o ponto médio pertence à diagonal, vamos usar esses valores conhecidos:

Simétrico de ( x , y ) em relação à ∆ é ( y , x ) , logo o ponto médio desses 2 é m 1 = ( x + y 2 , x + y 2 ) que também é o ponto A no nosso desenho

Simétrico de x , y em relação à ∆ ' é ( - y , - x ) , então o ponto médio do segmento que os liga é m 2 = x - y 2 , y - x 2 , que é o ponto B do desenho

Resposta

x + y 2 , x + y 2   e   x - y 2 , y - x 2  

Exercícios de Livros Relacionados

Faça um esboço dos seguintes planos: (a):2 x + 3 y + 5 z - 1 = 0
Faça um esboço dos seguintes planos: (b):x - 2 y + 4 z = 0
Faça um esboço dos seguintes planos: (e):3 x + 2 y - 1 = 0
Faça um esboço dos seguintes planos: (d):2 x + 3 z - 1 = 0
Faça um esboço dos seguintes planos: (g):3 z - 2 = 0