Várias vezes, nas páginas anteriores, foi citada e usada a propriedade de que as diagonais de um paralelogramo cortam-se mutuamente ao meio. Dado um paralelogramo , escolha um sistema de coordenadas adequado e use-o para provar a referida propriedade.

Faaaaala, galera! Prontos para mais uma questão?

Observe a figura abaixo.

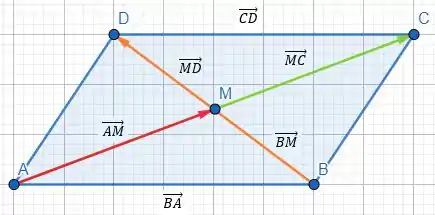
Considere o paralelogramo de lados , sendo uma de suas diagonais e o ponto médio de . Tome a outra diagonal do paralelogramo, . Devemos mostrar que o ponto também é ponto médio de , ou seja, .

Considere o vetor , este vetor pode ser escrito como a soma de dois outros vetores. Assim, , como é ponto médio de o vetor é igual ao vetor , como também .

Logo, podemos reescrever como:

Logo,

Logo, é o ponto médio em comum das duas diagonais

Até a próxima!