Dado o triângulo ABC, tome D na reta BC tal que C seja o ponto médio de BD e Y na reta AC tal que as retas AD e BY sejam paralelas. Exprima em função de e mostre que C é o ponto médio de AY.
Passo 1
Bora lá!
Primeiro, vamos fazer um esboço da nossa figura plana
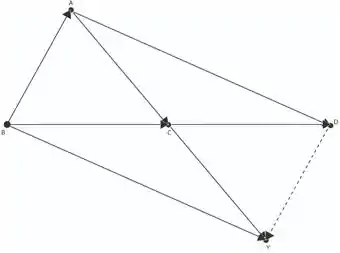
Agora, vamos exprimir em função de e mostre que C é o ponto médio de AY 😉.
Passo 2
Por hipótese, temos as seguintes informações:
- Todos os elementos estão em um mesmo plano
- Dado que ABC é um triângulo, logo seus lados e são linearmente independentes entre si, quando tomados de 2 a 2;
- são prolongamentos de e , respectivamente;
- Sendo o ponto médio do vetor , temos que ;
- e são paralelos, logo são múltiplos: .
Lembrando que exprimindo , temos
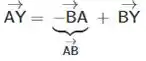
Mas como , sendo
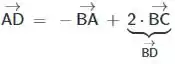
Então:
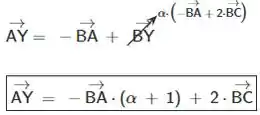
Passo 3
Agora para exprimir em função de precisamos determinar o coeficiente , certo? E para isso, vamos usar mais um vetor, .
Sabendo que tanto quanto somam , sendo , ou seja, sendo tais vetores paralelos (múltiplos), temos que um é a transladação do outro no plano , e portanto, para que as somas vetoriais sejam ambas iguais a ambos também têm que ser paralelos (múltiplos), associados por uma razão Assim, esses vetores também serão a transladação um do outro no plano , conservando a soma vetorial.
Passo 4
Logo,
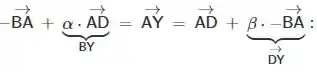
Mas e são linearmente independetes, pois é a junção do vértice do triângulo ABC ao prolongamento de um de seus lados,
Então, para tal combinação
Substituindo, temos:
E sabendo que (combinação linear de um triângulo), então:
logo é ponto médio de