Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 5.Exercício - Ex. 3a
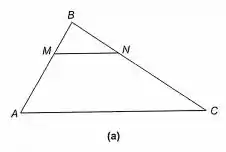
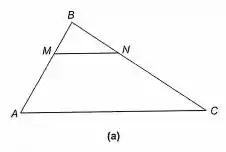
(a) No triângulo ABC da Figura 5-2 (a), M divide (A,B) e N divide (C,B) na mesma razão r. Prove MN//AC e calcule .
Passo 1
Bora lá!
Esse é o nosso triângulo ABC, onde M divide (A,B) e N divide (C,B) na mesma razão r:
Antes de matarmos esse exercício, vamos relembrar o que ele nos pede:
I – Prove MN//AC, ou seja, temos que provar que os segmentos MN e AC são PARALELOS;
II – Calcule , ou seja, temos que calcular a razão de sobre .
Beleza? Então, partiu!
Passo 2
Temos que provar a hipótese de que MN e AC são paralelos, então os triângulos BMN e BAC são semelhantes:
Portanto,
O enunciado nos diz que M divide (A,B) e N divide (C,B):
Portanto,
Passo 3
Da propriedade de proporção, temos:
Então de conseguimos obter a razão que queríamos
Passo 4
Já achamos a razão de , agora ficou mais tranquilo, vamos chamar essa razão de k, dessa forma, temos
Se
Resposta
(a) Isso provém de .