Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 20.Problemas - Ex. 2

Descreva precisamente a linha de nível zero da função ϕ : R²−→ R, dada por ϕ ( x ,   y )   =   x ³ -   y ³   -   x   -   y .

Passo 1

Olá galera! tudo bem?

Bora junto resolver mais um problema!

Este exercício não é nada trivial e vai requerer um pouco mais de domínio em álgebra de variáveis complexa.

Preparado?

Inicialmente nossa forma quadrática é x 3 -   y 3 -   x   -   y nesta equação vemos uma forma quadrática complexa composta de uma curva implícita.

Utilizando uma calculadora gráfica (Geogebra online) vamos obter o gráfico abaixo.

Veja que não é uma simples curva implícita, mas realizando x 3 -   y 3 -   x   -   y = 0 temos a linha de nível representada pela curva preta no gráfico.

Vamos dá uma boa olhada nela com um novo gráfico abaixo:

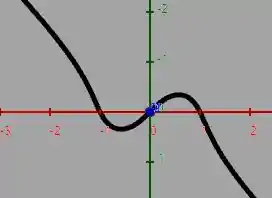
Observe que o mesmo pode ser representado (uma aproximação grosseira) que é a função f ( x ) =   s e n ( x )

Logo:

φ x , y = c ; com c   = λ 1 s 2 +   λ 2 t 2 ≈ s e n ( x )      

Te vejo na próxima questão!

Resposta

φ x , y = c ; com c   = λ 1 s 2 +   λ 2 t 2 ≈ s e n ( x )      

Exercícios de Livros Relacionados

Use o resultado do Exercício 18 para mostrar que se A = a b c d Então as soluções da equação característica de A são λ =1 2 a + d ± a - b 2 + 4 b c Use esse resultado para mostrar que A tem dois autov
Mostre que A e A T não precisam ter os mesmos autoespaços.
Suponha que o polinômio característico de alguma matriz A seja p λ = λ - 1 λ - 3 2 λ - 4 3 . Em cada parte responda à pergunta e explique ser raciocínio. A é invertível?
Seja A uma matriz 2x2. Dizemos que uma reta pela origem de R 2 é invariante por A se Ax estiver nessa reta sempre que x estiver. Em cada parte, obtenha as equações de todas as retas de R 2 que são inv
Mostre que a equação característica de uma matriz A de tamanho 2 x 2 pode ser expressa como λ 2 - t r A + det ⁡ A = 0 , onde t r ( A ) é o traço de A.