Enunciado
Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 1.Exercícios Propostos - Ex. 12
Desenhe dois vetores não paralelos e . Em seguida, desenhe , , , e . Escreva em função de e .
Passo 1
Fala, galera! Tudo beleza? Para resolver essa questão, temos que escolher os vetores e e, a partir deles, desenhar os outros vetores dados no enunciado. Nós vamos escolher como sendo um vetor que forma com a diagonal e aponta para cima e para a direita e como sendo um vetor horizontal que aponta para a direita:
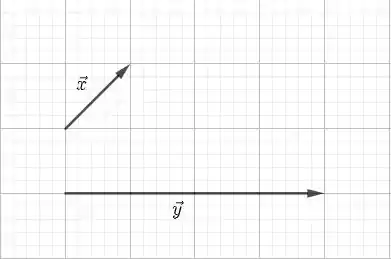
Essa escolha de vetores aqui é bem arbitrária e você pode ficar à vontade para escolher os seus vetores preferidos. O importante é a definição dos demais vetores.
Vamos começar desenhando , :
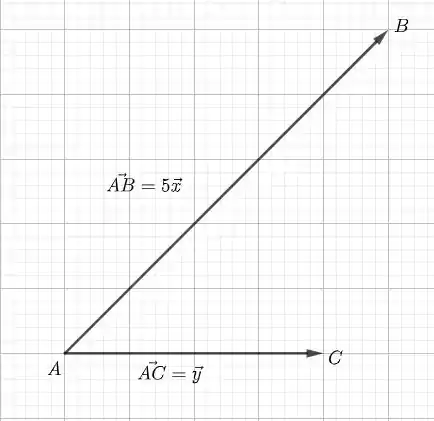
Passo 2
Agora, desenhamos e para obter :
Agora sabemos que é um vetor que faz com a horizontal e aponta para cima e para a esquerda. Lembrando que isso só vale para os vetores e que foram definidos lá no Passo 1. O ponto E é de onde o vetor sai até chegar no ponto C. Vamos aproveitar e já desenhar também :
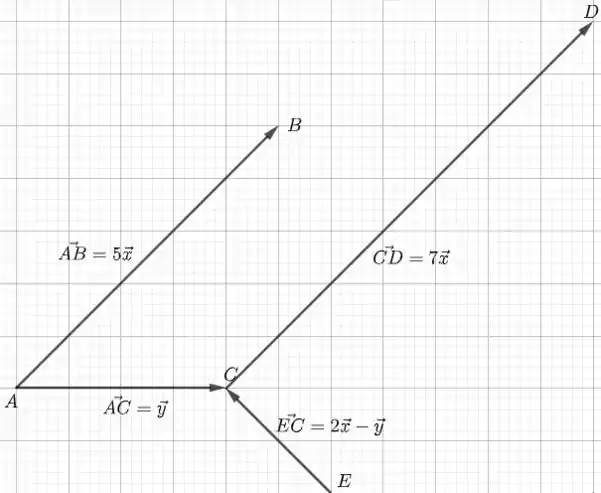
Passo 3
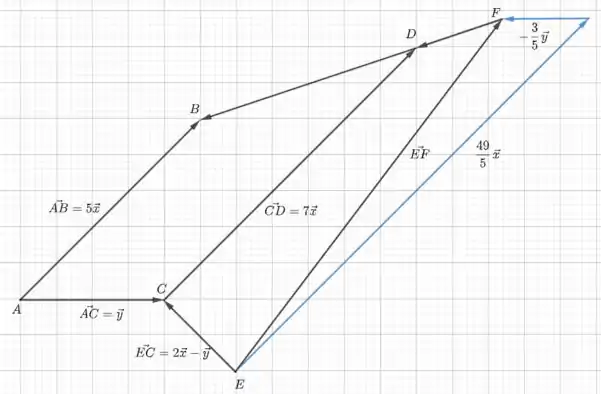
Agora, devemos notar que é o vetor que sai do ponto D ao B. Como , então está na mesma direção de e tem do seu tamanho. Aproveitamos também para desenhar o vetor , que é o que devemos calcular em termos de e . Pela figura abaixo, vemos que
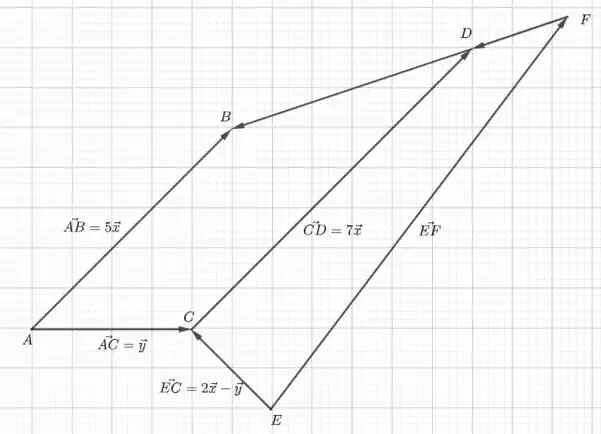
Nós já sabemos que , . Então, resta determinar . Como , na verdade temos que obter . Pela figura, podemos notar que
Agora, substituímos em :
Calma, ainda não acabou. Agora substituímos o resultado anterior e , em
Passo 4
Para confirmar que o resultado está correto, podemos desenhar e e mostrar que a soma desses vetores realmente dá (veja a figura abaixo). Ufa! Chegamos ao fim de mais uma questão, até a próxima!
