Enunciado
Álgebra Linear e Geometria Analítica - Reginaldo - Matrizes, Vetores e Geometria Analítica- Ed: 1º - Capítulo 1.1 - Ex. 3a
(a) AB é diferente de BA.
Passo 1
Bem pessoal, essa questão “a” está querendo saber se AB é diferente de BA, para sabermos isso temos que fazer as contas. Então vamos começar fazendo AB;
Para fazer a multiplicação de matrizes temos que pegar as linhas da primeira matriz e multiplicar pelas colunas da segunda matriz.
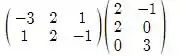
AB =
Fazendo a multiplicação então temos:
AB =
Simplificando temos:
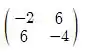
AB =
Passo 2
Agora precisamos fazer a multiplicação de BA.
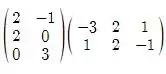
BA =
Fazendo a multiplicação vamos ter:
BA =
Simplificando temos:
BA =
Passo 3
Podemos concluir então que a matriz AB é diferente da matriz BA.
Resposta
A matriz AB é diferente da matriz BA.
Exercícios de Livros Relacionados
Usando a matriz α m do exercício anterior, efetue uma rotação dos eixos (mudança de coordenadas mantendo a origem fixa). Ache as novas coordenadas ( x ' , y ' , z ' ) dos pontos cujas coordenadas ( x
No exercício anterior, suponha que as coordenadas dadas são ( x ' , y ' , z ' ) . Quais eram, em cada caso, x,y,z?
Mostre que as matrizes A =1 1 y y 1 , em que y é um número real não nulo, verificam a equação X 2 = 2 X
Mostre que A e B são matrizes que comutam com a matriz M =0 1 - 1 0 , então A B = B A
Seja A = 1 0 5 1 1 1 0 1 - 4 . a)Encontre a solução geral do sistema A + 4 I 3 X =0 - b) Encontre a solução geral do sistema A - 2 I 3 X =0 -