Enunciado
Álgebra Linear e Geometria Analítica - Reginaldo - Matrizes, Vetores e Geometria Analítica- Ed: 1º - Capítulo 1.1 - Ex. 4
Verifique que x A1 + y A2 + z A3 = AX, em que Aj e a j-esima coluna de A, para j = 1, 2, 3
Passo 1
Essa questão é bem simples de resolver.
Precisamos fazer a multiplicação da matriz A com a matriz X.
Temos então:
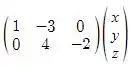
A*X =
Fazendo a multiplicação temos:
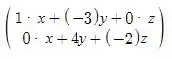
A*X =
Simplificando vamos ter:
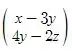
A*X =
Assim finalizamos a questão.
Resposta
A*X =
Exercícios de Livros Relacionados
2. Conhecendo-se somente os produtos AB e AC, como podemos calcular A(B + C), B t A t , C t A t e ( AB A)C?
(c) C D = d 1 C 1 d 2 C 2 d 3 C 3 , em que C 1 = - 2 0 - 1 , C 2 = 1 1 0 e C 3 = 1 1 1 , são as colunas de C .
(b) AEj é a j-esima coluna de A, para j = 1, 2, 3 e E B é a i-esima linha de B, para i = 1, 2, 3
(f) escrevendo A em termo das suas linhas A 1 = - 3 2 1 e A 2 = 1 2 - 1 , o produto A B pode ser escrito como A B = A 1 A 2 B = A 1 B A 2 B (o caso geral está no Exercício 1.1 17 (b) na página 23).
2.1.1. Seja A uma matriz 3 × 3. Suponha que X = 1 - 2 3 é solução do sistema homogêneo A X =Ō A matriz A é singular ou não? Justifique.